Capture183

ĄiuIi/j trendu wtnj anol\ut>

Wielomiany ortogonalne (orthóKonal /*>lynnmiah)

Zalc/nrtci kwadratowe, vwjicknt>e, kwarty c/nc (yiuidruitc. cubic auam Metoda SchcfTćgo \Schrfff* mr/Wi    '

Test Tukcya iTukty't test)

Rozstęp siudentytowany [studenti&d ruttgf)

Metoda Newmana-KcuIsj [NfHimin-Keuit mrilunl)

T01 wielokrotnego rozstępu Duncana \J)uncon’.i multiple rwiff* trir)

Zadania

1. W pewnym eksperymencie uzyskano następujące dane

	i	II	III	IV
fl	15	15	15	15
T,	87	160	188	66
X	5.80	10.67	1233	4.40
i*i #*i	640	1 700	2 800	500

Zastosuj metodę porównań ortogonalnych w celu porównania A’, / oraz + -V₄ z X_: + X).

2. W pewnym eksperymencie uzyskano następujące dane:

I    II    III

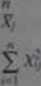
20    20    20~

7.40    10.5    12.65

2 156    2150    2 760

Oblicz sumy kwadratów: ta) wewnątrzgrupową. trendu liniowego oraz odchy lenia, tb> trzy oszacowania wariancji, (c) statystykę F d»> badanu isn-tn «. regresji liniowej oraz odchyleń od regresji liniowej.

3.    Określ nachylenie trendu liniowego dla danych z. zadania I. przyjmując jednostkową różnicę między poziomami zmiennej manipulacyjnej.

4.    Jakie są współczynniki dla wielomianów ortogonalnych r,_r o, oraz <, przy i =b’

5.    W pewnym eksperymencie uzyskano następujące dane:

	i	II	III	IV	V
n	10	10	10	10	10
X,	530	8.65	10.43	4.86	9.50
Ś4	305	875	1050	305	905

Oblicz trend liniowy, trend kwadratowy, trend sześcienny, odchylenie oraz | wariancję wewnątr/grupową i przeprowadź odpowiednie testy istotności

^ * pewnym eksperymencie uzyskano następ,,,* , ,_Jirw

1	n	III	IV	V
5	5 *.40	IS •	29.30	11.41)

<«d»i    ' *4 =    , wyml ,_v,_lK(„ _f

, 23.81. Pmównaj <rcdmc parami, stosując procedur* Scheffego Wtkaz kt/#_c -*4 »'^{,0,nc nu} P°^{z,om,c <)}•^0, -

₇ ^stosuj procedur* Newmana-Kculta do danych / zadania <5 , _Włka/ które jo/nice M »^s,°^{,nc n;i} P⁰²*⁰®*® ^{0 01}

</ajtoMJj procedur* Schcffćgo do danych z zadania 3 u ro/d/iaJe 15 w»kaz _uółt ró/nicc są islotne na po/romic 0.01

♦.Omów główne różnice między porównaniami planowanym, a po^wrunum, ptfhoc-

,₀ Co to je* kontrast^ł Podaj definicję . wyjaśnij. dlaczego pojęcie u, odjnwa Ajzną rolę w procedurach porównań wielokrotnych

|| Pr/yputómy. że w pewnym eksperymencie o schemacie 2 - 4 ,xr/yrTuno na ^ępuj^ce średnic z kratek:

/?< lh

Przyjmij n = 3 i - 2.

x Oblicz sum* kwadratów z wierszy, określając odpowiedni kontrast.

i przeprowadź test efektu głównego ogólnego R na poziomie u = 0.05 h. Określ zbiory wag dla kontrastów, których efekty łączne ^ równoważne elektowi głów nemu prostemu C w obrębie R_:

c.    Określ zbiory wag dla kontrastów , który ch efekty łączne są równoważne efektowi interakcyjnemu między R a C.

d.    Określ zbiór wag dla kontrastu ortogonalnego względem kontrastów z h i ic).

UPonitej podano prosty przykład planu dwuczynmkowcgo / gnjpami niezależnymi. Czynnik A ma dwa poziomy, a czynnik B trzy poziomy.

A*f\	K;B	AiH;	A:B:	AiBj
2	2	ft	3	1
3	0	6	2	2
4	1	II	1	0

A .By

4

3

5

a. Sporządź zbiór wag kontrastów (określonych na podstawie sześciu średnich / kratek) reprezentujących różnic* między średnimi brzegowymi czynnika A

VlS

363