img282

Odpowiedni schemat analizy wariancji w regresji wielomianowej według wielomianów ortogonalnych zawiera poniższa tabela (symbolem var £ oznaczono zmienność resztową błędu).

Błędy współczynników regresji aj obliczamy teraz ze wzoru

Źródło zmienności	Liczba stopni swobody	Suma kwadratów	Średni kwadrat	F etnp
Regresja w tym	P	var R	4	Ą/s^2,
regr. liniowa	1	var Rx	4,
regr. kwadrat.	1	var R2
Odchylenia od regresji	n - p — 1	var £		—
Ogółem	n - 1	var y	—	—

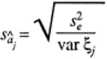
nie ma jednak potrzeby sprawdzania żadnej z hipotez szczegółowych

"o,^:a, = 0

gdyż są one sprawdzane w analizie wariancji. Hipotezę H₀j odrzucamy, gdy

^SR

r&p=^^> rcu,n.

Gdy rozpatrujemy regresję wielomianową, zmiennymi niezależnymi będą kolejne potęgi .t, istnieje więc naturalne uszeregowanie tych zmiennych. Wprowadzając zatem kolejne potęgi zmiennej x, można zbadać na podstawie schematu analizy regresji podanego w tabeli, czy wzrost dokładności równania regresji jest statystycznie istotny. Należy jednak pamiętać, że jeżeli na przykład, dołączenie kwadratu zmiennej nie zwiększy statystycznie dokładności regresji, nic będzie to oznaczało, że wpływ następnej potęgi także nie będzie istotny.

282