img110
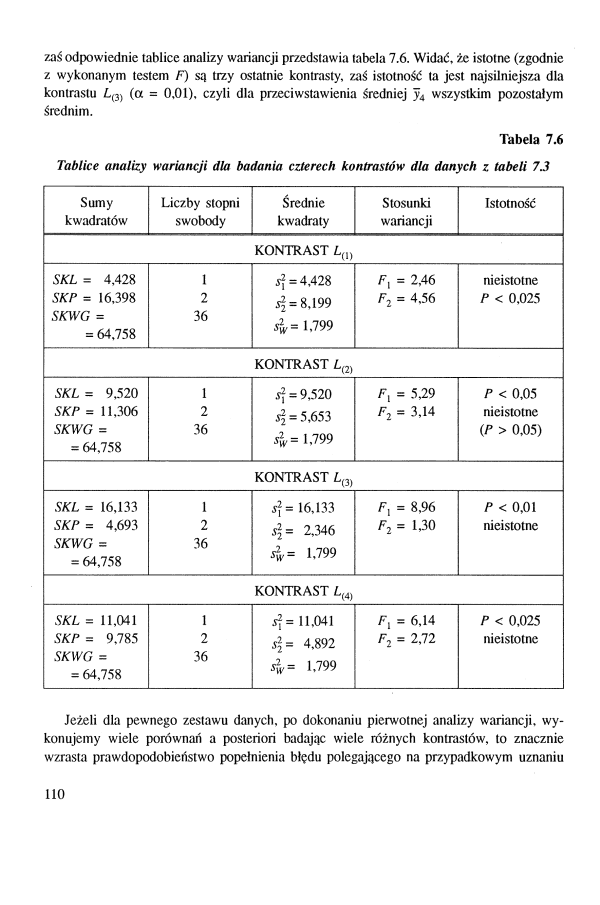
zaś odpowiednie tablice analizy wariancji przedstawia tabela 7.6. Widać, żc istotne (zgodnie z wykonanym testem F) sq trzy ostatnie kontrasty, zaś istotność ta jest najsilniejsza dla kontrastu L(3) (a = 0,01), czyli dla przeciwstawienia średniej y4 wszystkim pozostałym średnim.
Tabela 7.6
Tablice analizy wariancji dla badania czterech kontrastów dla danych z tabeli 7.3
|
Sumy |
Liczby stopni |
Średnie |
Stosunki |
Istotność |
|
kwadratów |
swobody |
kwadraty |
wariancji | |
|
KONTRAST L(I) | ||||
|
SKL = 4,428 |
1 |
Jj = 4,428 |
F{ = 2.46 |
nieistotne |
|
SKP = 16,398 |
2 |
4 = 8.199 |
F2 = 4,56 |
/> < 0,025 |
|
SKWG = = 64,758 |
36 |
4= 1,799 | ||
|
KONTRAST LQ) | ||||
|
SKL = 9,520 |
1 |
4 = 9,520 |
F{ = 5,29 |
/> < 0,05 |
|
SKP = 11,306 |
2 |
4 = 5,653 |
F2 = 3,14 |
nieistotne |
|
SKWG = = 64.758 |
36 |
s2w= 1,799 |
(P > 0,05) | |
|
KONTRAST L(3) | ||||
|
SKL = 16,133 |
1 |
*?= 16,133 |
u oo |
P < 0,01 |
|
SKP = 4,693 |
2 |
4= 2,346 |
F2 = 1,30 |
nieistotne |
|
SKWG = = 64,758 |
36 |
4= 1,799 | ||
|
KONTRAST L(4) | ||||
|
SKL = 11,041 |
1 |
4= 11,041 |
F, = 6,14 |
P < 0,025 |
|
SKP = 9,785 |
2 |
4= 4,892 |
F2 = 2,72 |
nieistotne |
|
SKWG = = 64,758 |
36 |
4= 1,799 | ||
Jeżeli dla pewnego zestawu danych, po dokonaniu pierwotnej analizy wariancji, wykonujemy wiele porównań a posteriori badając wiele różnych kontrastów, to znacznie wzrasta prawdopodobieństwo popełnienia błędu polegającego na przypadkowym uznaniu
110
Wyszukiwarka
Podobne podstrony:
img110 zaś odpowiednie tablice analizy wariancji przedstawia tabela 7.6. Widać, żc istotne (zgodnie
img163 Tablicę analizy wariancji pokazuje tabela 8.9. Tabela 8.9 Tablica analizy wariancji przedstaw
img109 Tabela 7.5 Tablica analizy wariancji dla badania istotności kontrastu liniowego
img120 Tabela 7.12 Tablica analizy wariancji dla danych z tabeli 7.11 Źródło Suma Liczba
img126 Tabela 7.16 Tablica analizy wariancji dla danych z tabeli 7.J5 Źródło Suma Liczba
img131 Tabela 7.20 Tablica analizy wariancji dla wyników badan liczby chloroplastów w komórkach mchu
img152 Tabela 8.3 Tablica analizy wariancji dla regresji liniowej z testem na
img154 Tabela 8.5 Tablica analizy wariancji dla regresji liniowej z testem na liniowość (dla danych
img245 Tabela 11.2 Tablica analizy wariancji w przypadku dwuczynnikowym jednowymiarowym Sumy
więcej podobnych podstron