img126

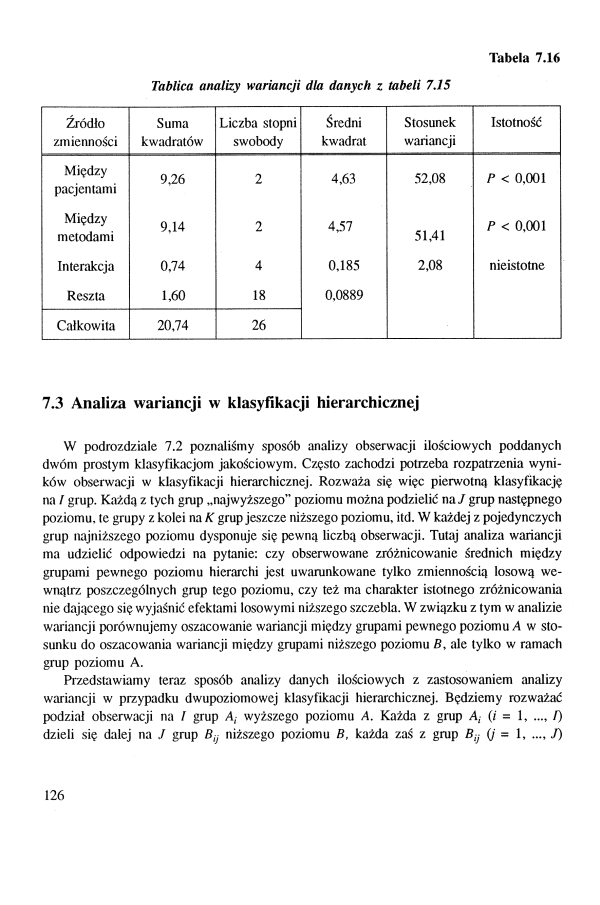
Tabela 7.16

Tablica analizy wariancji dla danych z tabeli 7.J5

Źródło	Suma	Liczba stopni	Średni	Stosunek	Istotność
zmienności	kwadratów	swobody	kwadrat	wariancji
Między pacjentami	9,26	2	4,63	52,08	P < 0,001
Między metodami	9.14	2	4,57	51,41	P < 0,001
Interakcja	0,74	4	0,185	2,08	nieistotne
Reszta	1,60	18	0,0889
Całkowita	20,74	26

7.3 Analiza wariancji w klasyfikacji hierarchicznej

W podrozdziale 7.2 poznaliśmy sposób analizy obserwacji ilościowych poddanych dwóm prostym klasyfikacjom jakościowym. Często zachodzi potrzeba rozpatrzenia wyników obserwacji w klasyfikacji hierarchicznej. Rozważa się więc pierwotna klasyfikację na ! grup. Każda z tych grup „najwyższego" poziomu można podzielić na / grup następnego poziomu, te grupy z kolei na K grup jeszcze niższego poziomu, itd. W każdej z pojedynczych grup najniższego poziomu dysponuje się pewna liczba obserwacji. Tutaj analiza wariancji ma udzielić odpowiedzi na pytanie: czy obserwowane zróżnicowanie średnich między grupami pewnego poziomu hicrarchi jest uwarunkowane tylko zmiennością losową wewnątrz poszczególnych grup tego poziomu, czy też ma charakter istotnego zróżnicowania nie dającego się wyjaśnić efektami losowymi niższego szczebla. W związku z tym w analizie wariancji porównujemy oszacowanie wariancji między grupami pewnego poziomu A w stosunku do oszacowania wariancji między grupami niższego poziomu B, ale tylko w ramach grup poziomu A.

Przedstawiamy teraz sposób analizy danych ilościowych z zastosowaniem analizy wariancji w przypadku dwupoziomowej klasyfikacji hierarchicznej. Będziemy rozważać podział obserwacji na I grup A, wyższego poziomu A. Każda z grup Ą (/' = 1, ...» f) dzieli się dalej na J grup B_i} niższego poziomu B, każda zaś z grup B_i} (j -    .... J)

126