Capture263

uwagę, wyników standardów

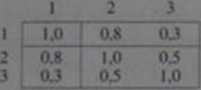
Zmienna 1 stanowi kryterium, a zmienne 2 i 3 sq predyktoran, / gę. ze wartości 1.0 umieszczone są na głównej przekątnej W _cclu .    ~

irdowych w zakresie zmiennych 2 i 3 z osobna. ro/wi^C-równania regresji :/ = 0.8:. i ż/ = 0.3:,. Zmienna 2 jest znacznie lep>/._r klonem ni/ zmienna 3. Prawdopodobnie na podstawie znajomości wbu iy h ,Vl nych bylibyśmy w stanie lepiej oszacować wartość kryterium

W jaki sposób możemy otrzymać zbiór wag. które zmaksymalizują l._:,_x między kryterium a sumą wyników w zakresie zmiennych niezależnych> Ozrs. -wagi sy mbolami p_: i p_t. Oszacowania wyniku standardowego w /akrc-ie 1 dokonujemy na podstawie równania = (¹>:, + Chcemy oblic/yc m .ę Pj i P>. aby korelacja między :, i a była jak największa. Z punktu u,Jat-

matycznego problem ten sprowadza się do obliczenia wag. które zminimalizuj.¹ većr.. sumę kwadratów różnic między wynikiem w zakresie kryterium a w¹. wyniku w zakresie kryterium Potrzebne są nam takie wartości wag. aby

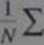
Ui - z\)r =

minimum.

Wartości P; i pj są wagami regresji wielokrotnej dla wyników standard.--.! Bywają one nazywane wagami beta.

Przy trzech zmiennych¹ wartości py i p, wyrażone są wzorami

P:

Pi

^13^23

ni

^r\2^r2i

1

(2651

(24f¹

ny

p, * 91    10,5

■ 0.867 * -0.133

I - 03J

^ » 9jŁr_0* x OJ I - Oi^ł ~

Pomarzmy tim« przez

Zapiwmy te wagi u góry i / boku tabeli korel*,. . kolumny w następujmy sposób.

0.H67 -O.I33

0.S67

-0.133

IjOB) TOAM _Qjmo OM*' Q7«

-OjO« -0.05*    0011

Sumy elementów w ćwiartkach tabeli ^ następujące

1.000	0.654
0.654	0.654

Korelacja między kryicnum a suma wag wynosi:

C 0.654    -

m" v?m'^v0-⁶⁵⁴ ■ ⁰-⁸⁰‘'

Jest 10 współczynnik korelacji wielokrotnej. Możemy oznaczyć go symbolem R Żaden inny system wag nie da nam silniejs/cj korelacji między kntenum a suma ważioną predyktorów.

Zwróćmy uwagę, żc suma elementów w górnej prawej ćwurtcc tabeli korelacji ważonych równa jest sumie elementów w jej dolnej prawej ćwiartce, czyli C = łi Dzieje się tak. gdy zastosowane wagi sa wagami regresji wielokrotnej. Pozwala nam to sprawdzić prawidłowość przeprowadzonych obliczeń. Zauważmy też. że /?- = C. a R = 'lc. Zatem współczynnik korelacji wielokrotnej możemy otrzymać na podstawie wzoru:

R = ^,2 + piTu •    (26.7)

Jest to powszechnie stosowany wzór na obliczanie współczynnika korelacji wielokrotnej.

Współczynik korelacji wielokrotnej R interpretuje się tak samo jak współczynnik korelacji r. Jest on miara związku między zmienna zalczna a ważonym zbiorem zmiennych niezależnych o wagach wybranych tak. ab> zmaksymalizować R.R- jot proporcją, tak samo jak r. R^: jest proporcją zmienność, zmiennej zależnej, którą można wyjaśnić bądź przewidzieć na podstawie ważonej sumy zmiennych niezależnych. W przykładach, które omówiliśmy wyżej. R - 0.809. a R- * 0.6. A

523

1

A dwóch zmiennych niezależnych. prcdykloraJi (przyp red nauk )