CCF03252008001

^x\

x.

X

— wektor zmiennych decyzyjnych,

c = [C[ c₂... cj — wektor wag funkcji celu.

Podstawowym zabiegiem stosowanym przy rozwiązywaniu zadań decyzyjnych jest sprowadzanie ich do równoważnej, lecz wygodniejszej ze względów numerycznych postaci. Dla zadania PL rozwiązywanego metodą simpleks będzie to postać kanoniczna.

Aby uzyskać równoważną dla danego zadania postać kanoniczną, nierówności sprowadzamy do równości wprowadzając' tzw.zmienną swobodną. Z każdym warunkiem w postaci nierówności związana będzie właściwa temu warunkowi zmienna swobodna równoważąca jego stronę lewą z prawą. Zmienne te do funkcji celu wchodzą z zerowymi wagami.

Jeżeli w zadaniu PL jest nierówność (2.27) typu/^ tó zmienną swobodną x„ _{+ f} ^ 0 oznaczamy jako:

r i

1= i

<

Jeżeli natomiast w zadaniu PL jest nierówność typu ^, to zmienną swobodną x„ _{+ i} 5= 0 definiujemy jako:

n

^xn*t = I a_ijXj -

PRZYKŁAD 2.6 Mamy następujące zadanie PL:

— 2xj + 4x₂ + 2x₃ -> max, n

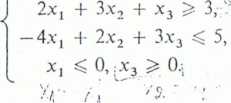
o .

/

(2.33)

■x;

Aby zadanie (2.33) zapisać w równoważnej postaci kanonicznej, należy obydwie nierówności sprowadzić do równości oraz na wszystkie zmienne nałożyć warunki nieujcmności. W tym celu wprowadzamy:

(a)    zmienne swobodne x₄ i x₅,

(b)    zmienne X/, x₂', x₂" zamiast zmiennych x,, x₂; x, = — x/, x₂ = x₂' —x₂".

Równoważną postać kanoniczną zapiszemy więc następująco:

2x,' + 4(x₂' - x₂") + 2x₃ + 0x₄ + 0x₅ -» max, J -2x/ + 3(x₂' - x₂") + x₃ - x₄ + 0x₅ = 3,

4x/ + 2(x₂' - x₂") + 3x₃ + 0x₄ + x₅ = 5,

^A’l > ^x2 ’ ^X2 > *31    ^X5 ^ 0-

Jeżeli mamy zadanie PL z funkcją celu:

n

Z CjXj -> max, j=i

to równoważne mu będzie zadanie z funkcją celu:

fl

I {~Cj)Xj -> min.

2.4

Dualność

2.4.1

Reguły tworzenia zadania dualnego

Z każdym zadaniem PL sprzężone jest pewne inne zadanie PL zwane zadaniem dualnym (ZD). Jeżeli zadaniem pierwotnym (ZP) jest zadanie:

r

n

I CjXj - max, j= i

1 t a_tjXj < fc, (/= 1,2.....m),    “    (2.34)

y= i

Xj- ^ 0    0* = 1,2.....«),

to zadaniem dualnym będzie zadanie:

™    fi -1c- V / '    '

I b. y,- -» min,

i = 1

(2.35)

J    £

I Z "ij-y,- > ^cr 0' = i,2,...,n),

i = 1

y_t> 0 (i = 1,2.....m).

Z relacji zachodzących między zadaniem pierwotnym a zadaniem dualnym wynika, że: