CCF20140608004

2.2. Odwzorowania zwężające 27

= sup{|xi(£) — X2(f)|: t £ [0/1]}/ jest przestrzenią zupełną. Jeśli zamiast wszystkich funkcji ciągłych weźmiemy zbiór wielomianów algebraicznych, to przestrzeń nie będzie zupełna. Jeżeli natomiast zamiast wszystkich wielomianów weźmiemy zbiór wielomianów stopnia nie większego niż N (gdzie N < oo), to przestrzeń będzie zupełna (granica jednostajnie zbieżnego ciągu wielomianów stopnia nie większego od N jest wielomianem stopnia nie większego od N).

Płaszczyzna euklidesowa R², w której odległość między dwoma punktami zi = (x\,y\) i Z2 = (*2,1/2) l^est określona wzorem

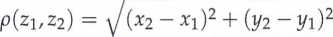
(albo płaszczyzna zmiennej zespolonej, gdzie p(zi,Z2) = |z2 — Zj |), jest przestrzenią metryczną zupełną. Każdy domknięty i ograniczony podzbiór płaszczyzny euklidesowej również jest przestrzenią metryczną zupełną.

Definicja 2.3. Operację f nazywamy zwężającą w przestrzeni metrycznej (X, p), jeśli dla dowolnego x £ X mamy f(x) £ X i jeśli istnieje taka liczba A £ (0,1), że dla dowolnych x\, xi £ X spełniony jest warunek Lipschitza

(2.7)

p(f(xi),f(x₂)) Xp{xi,x₂)

Rozwiązanie Xoo równania x = f(x) jest nazywane punktem stałym operacji (odwzorowania) /.

Twierdzenie 2.1 (Banacha o odwzorowaniach zwężających). W przestrzeni metrycznej zupełnej (X,p) operacja zwężająca ma dokładnie jeden punkt stały *00. jest on granicą ciągu xq, x\, *2, • • •, gdzie *0 j^est dowolnym elementem zbioru X, a x_n+i — f{x_n). Zachodzi oszacowanie

(2.8)

p(x_n,X_co) < ^—^p(*o,*l)

Często rozważa się operacje / zależne od jakiegoś parametru. Parametrem może być liczba należąca do jakiegoś przedziału lub, ogólniej, element jakiegoś zbioru, w którym zdefiniowano odległość między wartościami parametru. Interesuje nas wówczas zależność rozwiązania od tego parametru. Przytoczymy jedno z twierdzeń, w którym sformułowano założenia, przy których mała zmiana parametru powoduje małą zmianę rozwiązania.

Twierdzenie 2.2. Rozważmy w przestrzeni metrycznej zupełnej (X,p) równanie x = f(x;z) zależne od parametru z należącego do przestrzeni metrycznej (Z,p_z). Załóżmy, że

1) /(X;Z) C X,