img029

29

gdzie L Jest liczbą dodatni? mniejazę od jedności. Funkcja f Jest więc odwzorowaniem zwężajęcyre w przestrzeni zupełnej    i na podste-

wie twierdzenia Banacha stwierdzamy, żs równanie f(x) * x ma dokładnie jedno rozwiązanie x * r, które ,-nożna znaleźć w sposób przybliżony, bioręc dowolr.ę liczbę x_Q i tworzęc clęg kolejnych przybliżeń x^^ •

«* f(x_p), ><₂ “    . Cięg x_Q,x₁,... jest zbieżny do r w sensie

metryki d_k(a,b) ■    l oraz

^dk<^xi'^r) ^ 7-rr ^dk⁽’v^xo⁾

{dlaczego?) •

y|

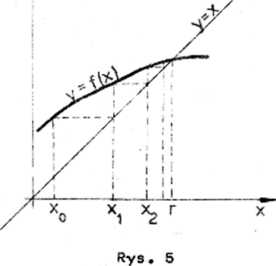
Na rysunku 5 pokazano wykres funkcji spełniajęcej warunek (2.11) ze stałę L mniejszę od jedności oraz konstrukcję cięgu x₀,x^,..# . Widać, że liczby *o'^xl'^x2^#    9ię do odciętej

r punktu przecięcia wykresu funkcji f z. przekętnę pierwszej i trzeciej ćwlart ki płaszczyzny euklidesowej* Proponuję również sprawdzenie na odpowiednio sporządzonym rysunku, że jeśli wykres funk cji f Jest zbyt stromy, tzn, funkcje f nie spełnia warunku (2.11) ze stałę L mniejszę od Jedności, to przy odpowiednim wyborze liczby x₀ skonstruowany cięc x_o,x_1#... może nie tylko nie być zbieżny do r, a nawet może być rozbieżny.

Wskazane metoda przybliżona nosi nazwę metody kolejnych przybliżeń i ma duże znaczenie praktyczne, 'zęsto wyznaczenie pierwszych kilku wyrazów cięgu kolejnych przybliżeń x, Xj«f(£), x₂»f($),... pozwala na obliczenie z duż? dokładności? poszukiwanego rozwięzania równania x *

* f(x)»

Metoda kolejnych przybliżeń oraz inne metody przybliżone rozwięzywa-nia nie tylko równań algebraicznych omawiane sę szczegółowo w jednym z ważnych działów matematyki, a mianowicie w metodach numerycznych.

2. Przypuśćmy, że mamy rozwięzać układ n równań liliowych o n nie wiadomych

°ll^xl *    ^a12^x2    *    •••    *    ⁸ln^xn    "    ^bl>

^a21^xł *    ^a22^x2    *    **•    ^ł    a2n^xn    *    ^b2>

^ant^xl *    ^sn2^x2    ^ł    •••    ^ł    ann^xn    *    ^bn'