CCF20160103000

H	Funkcje wymierne		Klasa ll_
p			Wersja A
	Imię i nazwisko	Wynik pkt. Ocena
Zad. I.	Wersja trudniejsza	Wersja łatwiejsza Zad. 1.

Dana jest funkcja f(x)-

2x-3 ' x-l '

Wyznacz.dziedzinę funkcji wymiernej:

1.

a)    Wyznacz dziedzinę i miejsca zerowe funkcji/.

b)    Dla jakiego argumentu funkcja/przyjmuje wartość 4?

2x~ +5x+3

Podaj przykład funkcji wymiernej, której dziedziną jest zbiór /f\{0,1}.    '

2 3x

A+l X—l

Zad. II.    *

_2 y — 5

Dana jest funkcja /(x) = —- .

a)    Sporządź wykres funkcji /

b)    Wyznacz przedziały monotoniczności funkcji.

c)    Dla jakich argumentów funkcja przyjmuje wartości dodatnie?

Zad. 2.

Wykonaj działania i sprowadź’do najprostszej postaci:

O (_ 1

-3x x + x

Zad. III.

Rozwiąż równanie

jc + 3 x + 2

-1 = -

x—3

Zad. IV.

Rozwiąż nierówności: 3-t + l .

a)

b)

2x-5

x-5

>0,

12

-4x

-5    * + 1

Zad. 3.

9

Dana jest funkcja /(z) = 1-1——.

a)    Sporządź wykres funkcji/ -

b)    Określ dziedzinę i zbiór wartości funkcji.

c)    Wyznacz przedziały monotoniczności funkcji.

d)    Dla jakich argumentów funkcja przyjmuje wartości dodatnie?

Zad. 4.

Dana jest funkcja g (x) = -

-4

Zad. V.

Dwie koparki, pracując jednocześnie, mogą wykonać pracę w ciągu 12 dni. Jedna z koparek po 10 dniach popsuła się i pracę dokończono przy użyciu drugiej koparki w ciągu 5 dni. Ile potrzebuje każda z koparek na wykonanie tej pracy samodzielnie?

a)    Oblicz wartość funkcji g dla argumentu 1.

b)    Wyznacz miejsca zerowe funkcji g.

Uwaga! Możesz podwyższyć ocenę, jeśli dodatkowo rozwiążesz zadanie IVb z wersji trudniejszej.

p		Funkcje wymierne	Klasa 5I_
			Wersja 8
	imię i nazwisko	Wynik pkt Ocena

.    Wersja trudniejsza

Zad. I.

Dana jest funkcja f(x) = — — * -1.

a)    Wyznacz dziedzinę i miejsca zerowe funkcji/.

b)    Dla jakiego argumentu funkcja/przyjmuje wartość 5?

Wersja łatwiejsza

Zad. 1.

Wyznacz dziedzinę funkcji wymiernej:

Podaj przykład funkcji wymiernej, której dziedziną jest zbiór R \ {-3,0}.

a)

b)

Zad. II.

3r —l

Dana jest funkcja f{x) = ———.

a)    Sporządź wykres funkcji/.

b)    Wyznacz przedziały monotoniczności funkcji.

c)    Dla jakich argumentów funkcja przyjmuje wartości ujemne?

Zad. 2.

Wykonaj działania i sprowadź do najprostszej postaci:

1    , 2r-3

x-2    x+2

'-x.3x-3 ^:_9' x + 3

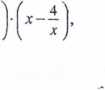
Zad. III.

Rozwiąż równanie

3    . . x² + 5 ,

x — 1

- + 5 = -

4.r-l x +1

Zad. IV.

Rozwiąż nierówności-1-3*

a)

2*-4

<0,

Zad. 3.

Dana jest funkcja / (*) = 1--!—.

x-2

a)    Sporządź wykres funkcji /.

b)    Określ dziedzinę i zbiór wartości funkcji.

c)    Wyznacz przedziały monotoniczności funkcji.

d)    Dla jakich argumentów funkcja przyjmuje wartości ujemne?

.. 35 — 7* *-4    1

x²-9 -r + 3    *-3'

Zad. V.

Jedna sekretarka może wykonać pewną pracę w czasie o 6 godzin krótszym niż druga sekretarka. Obie, pracując równocześnie, mogą tę pracę wykonać w ciągu 4 godzin. Ile godzin potrzebuje każda z nich na wykonanie danej pracy samodzielnie?

Zad. 4.

2 _

Dana jest funkcja g (*) = ————.

x~ -1

a)    Oblicz wartość funkcji g dla argumentu 2.

b)    Wyznacz miejsca zerowe funkcji g.

Uwaga! Możesz podwyższyć ocenę, jeśli dodatkowo rozwiążesz zadanie IVb z wersji trudniejszej.

27