DSC00798

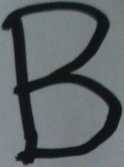
USM Matematyka - egzamin Grupa B

Zadanie 1 (3 punkty)

Rozwiązać następujące zagadnienie początkowe:

y^m - 2y" + y' - 2y = 0, ;y(0) 11, / (0) = 0, y”(0) 10.

Zadanie 2 (5 punktów)

Znaleźć rozwiązanie ogólne równania:

y'+y=e^x + x

Zadanie 3 (2 punkty)

Znaleźć zbiory, w którym równanie

u^ + (2 cos x)u_xy - [sin² x)*yy - (sin x)u_y = 0

jest typu hiperbolicznego, parabolicznego, eliptycznego.

Zadanie 4 (2 punkty)

Rozwiązać następujące zagadnienia brzegowe:

«xx(^3^,)=°»    “(o ,y)=y²,    «(!,)')=i

Zadanie 5 (5 punktów)

Stosując metodę rozdzielania zmiennych znaleźć rozwiązanie równania

u xx =u_tt    , 0 < x < c, t > 0

Z warunkami: u(0,f) = 0, u(c,f) = 1, M_f(x,0) = 0-

Zadanie 6 (3 punkty)

Stosując następujący wzór d’Alemberta:

30-01-10 11:42

x+at

f(x-at) + f(x + at) + - J g{z)dz

x-at

Znaleźć rozwiązanie następującego zagadnienia brzegowego:

d^2u	2 d^2u
dt^2	= a dx^2

w(0,x) = /(x) = x;    —    8 g(x) | e~

Ot

a = 2.