DSC02832

7. ftinfcęia / (x)

(b) / (x) m l<un x\ <Jln x € (0,2*) nm minimum lokalne właściwe w punkcie xu =» »;

(b) może miał ekstrema loknlno tylko w punktach, w których jej pochodna równa się /ero albo w punktach, w których jaj poulaKinn nic istnie,jn;

w- ma w punkcie xo iimksinuim loknlno właściwo, jotell jent ciągło

w punkcie zę. rófcniczkownlnn w pewnym sąslcdzlwio »V(x_0l/>) tego punktu oraz f\ /* (x) >0 i /\    / (*) < 0.

8. Dla dowolnej funkcji / (x) prawdą j<s.l, że

(a)    funkcja /(x) maleje coraz szybciej w przedziale (a, 6), jeżeli jest malejąca i wypukła w tym przedziale (/ (x) < 0, / (x) > 0 dla

(b)    posługując się drugi) pochodną / (x) wyznacza się przedziały wklęsłości funkcji / (x) oraz punkty przegięcia wykresu lej funkcji;

(c)    prosta o rówuauiu y = b jest usyinptolą poziomą lewostronną wykrotu funkcji / (x) wtedy i tylko wtedy, gdy istnieje granica b = lim f (*V

«-*-oo * '

9. Czy poniższe całki są poprawnie obliczone:

(a) J x⁵ lnxdx = ix° In x + c\

>,* (^x x<Lc 1 —

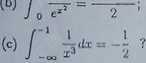
	’ 1 '		1 ‘		■ 1 ■
10. Dane są wektory: a =	0 0	,b =	1 0	1 ^c =	1 1

(n) Wektor n j«>sl kombinneją liniową wektorów b, c.

(b)    Wektory n, b, c nie tworzą buzy przestrzeni R³.

(c)    ||c||« 1.

Ili Dla dowolnych macierzy A wymiaru nxw, U wymiaru mxn, C wymiaru rl X U wykonalno są następujące działania:

(«) C | U • A;

(b) A • W • C;

' (c) C+A-D.