DSC07328

74

Macierze i

wyznaczniki

• Przykład* 3.15

Korzystając z algorytmu Chió obliczyć podane wyznaczniki:

6 3-2		; b)	13 5 2 2 4 7 -1
7 2	5		2-2 6 3
4 1	-2		4-3 1 1

[Rozwiązanie    -7-—;

Algorytm Chió pozwala obliczać wyznaczniki przez kolejne obniżanie ich stopni. y-znacznik macierzy kwadratowej A = [a,j\ stopnia n ^ 3, w której elemen “11 niezerowy. wyraża się wzorem

det A —

1

(•u)"'*

O33 Oą    “2r*

0)3 au - -. a₃„

gdzie

°y

aii a U    dla 2 ś ^

on

Od! Ofi3 ---®nn

	I 6 3 I I 6 -2 I
1	7 2 1 1 7 5 1
6*”*	I 6 3 I I 6 -2 I
	|4 1 | | 4 -2 |

a) Postępując zgodnie z algorytmem Chió otrzymamy

6	3 -2
	2 5
4	I -2

1 -0 44 “6 -6-4

3 -11 2 1

2.25 = 5°-

b) Stosując dwukrotnie algorytm Chió kolejno otrzymamy

				I 1 3 I		1 6		1		2 I
				2 4		2 7		2	.	1
1	3 6 2
2	4 7-1	1		1 3		1 5		1		2 I
2	-2 6 3	—	14-a '	1 2 -2		2 6		2		J 1
A	-3 1 1
				1 3		1 5		1
				| 4 -3		4 1		4		|
										-2
			-2	-3 -5	a |					-8
			-8	-4 -1
			-16	-19 -7	(-2)					-2

-2

—8

-5

-1

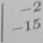
-5

-7

Przykłady    S

Macierz odwrotna

Przykład 3.16

Korzystając z twierdzenia o postaci macierzy odwrotnej znaleźć macierze odwrotne do podanych:

1+i    1

1 i-i

■i 2    5    7

a) A =

; b) .4 = 6    3    4

6 -2 - 3

Rozwiązanie

Wzór określający macierz odwrotną do nieosobliwej macierzy kwadratowej A stopnia n ma postać

	Du	Di, .	. Din '
1	Dn	Dn .	- Din
" dcl .4	. Dni	Dn, .	■ Dnn .

A" =

gdzie Dij oznacza dopełnienie algebraiczne elementu aij tej macierzy, a) Mamy

Zatem

	det ,4	= (! + '		-1^J =
Dn	= ' det [l-i|	= l-t	Du	= (-l)^,+,det		[i| = -
Dn	= (~l)^2+1 det (1| =	H	Dn	= (—l)^,+2det		|i+*1
-i _	1 [ Dn Di, '	T _ 1	1 —i	-1	T	1 —i
	det A [ D,, Di,	“ T	-1	1+i		-l

-1

dci,/i = |2• 3• (—3) + 5• <1 ■ 5 + 7-6- (—2)) — [7 -3 -5 + 2-4■ ( 2) + 6• 5• ( 3)J **

b) Mamy

Di i = (-i)^1+l	3 4 -2 -3	= -1,	Di, = (-0
Dn = (-1)^,+1	6 3 5 -2	= -27,	Di t = (-l)
Dn = (-1)^3+J	2 7 5 -3	= -41,	Dn = (-0
Dn == (-l)*^+l	5 7 1 3 % f	= -l,	Da = (-1)

s i

—2 -3

2 8 8 -2

2 7 0 4

Du = (—1)'

= -24.

0    4 =38,

5 -3

= 1, = 29, = 34,

2 5 6 3