egzamin matma4

47.

a) Narysować szkic wykresu funkcji y - arctg.r. h) Podać wartości dla: arctgO, arctg(l) i liin_t. ._>H ,_x arctgac c) Rozwiązać nierówność: aret.g(l (>:r) > 0.

48. Obliczyć granice ciągów i funkcji:

n -y/r lim    :

u—2/r* -I- o

b) lim

f*—>'X-

n

n - 1

d+i

,x sina lim.....-

X—*o

+ cos X

49. .

a)    Podać wzór na pochodną, funkcji złożonej i pochodną ilorazu funkcji.

b)    Wyznaczyć dziedziną i pochodną dla następującej funkcji:

F{x) - In

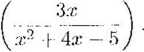
50. .

a)    Podać twierdzenie o monolouiczności funkcji.

b)    Wyznaczyć dziedziną. przedziały nionolonicznośei, ekstrema lokalne, dla funkcji:

f(x) ^

51. Wyznaczyć przedziały wypukłości, wklęsłości i punkty przegięcia dla funkcji:

./'(■'•) = ₁^-*⁴ x? ' 3z 4- 7.

4