IMG00163

163

fr - dopuszczalne bicie promieniowe zwoju mm fr-kd+1,

d - średnica podziałowa ślimaka, mm, k,l - współczynniki (tabl. 12.1.16).

2. Wysokość do cięciwy zwoju ślimaka (h_a) - najkrótsza odległość od wierzchołka zwoju ślimaka do środkowe-

Tabl. 12.1.15. Tolerancja grubości zwoju wzdłuż cięciwy T§

PN-80/M-88522.04

.2, o.	Dopuszczalne bicie promieniowe zwoju fr, fj.m
	>20	>25	>32	>40	>50	>60	>80	>100
Ile	<25	<32	<40	<50	<60	<80	<100	<125
(2 i	Tolerancja grubości zwoju wzdłuż cięciwy 7i, fim
h	32	38	42	50	60	70	90	110
d	42	48	55	65	75	90	110	130
c	52	60	70	80	95	110	140	170
b	65	75	85	100	120	130	170	200
a	85	95	110	130	150	180	220	260

Tabl. 12.1.16. Zależność k, 1 = f (klasa dokładności)

Kasa dokładności	k	1
7	0,070	15,0
8	0,110	23,8
9	0,174	37,6

go punktu grubości zwoju po cięciwie, mm (rys. 12.1.6) h_a=h'_am + 0,5 5„tg (0,5 arc sin (5„ tg^{1 2}7/d))-

PRZYKLAP 6. Ślimak o klasie dokładności 7-C, m = 8 mm, (rys. 12.4.5)    d = 64 mm, 7= 14°2', a_w= 192 mm.

S„= l,571rn-cos7 = 1,571-8 0,9703 = 12,195 mm;

E&= 0,12 mm; = 0,09 mm;

£■*5= 0,12+0,09 = 0,21 mm; A = 0,07; C = 15; fr = 0,07-54+15= 18,8 /im; 7# =0,045 mm;

5=( Ś„-E,_s)-T_ś = (12,195- 0,21)-8_i045=l 1,985-_o⁰o45 ^m

12.2. KONSTRUOWANIE ZĘBATYCH KÓŁ WALCOWYCH, wg [15,24,38,52] 12.2.1. OBLICZANIE NIEKTÓRYCH PARAMETRÓW GEOMETRYCZNYCH

1. OBLICZANIE WSPÓŁCZYNNIKÓW PRZESUNIĘCIA i X₂ DLA ZADANEJ ODLEGŁOŚCI OSI d_w

Tabl. 12.2.1

Odległość osi podziałowa	o	Q_m(z,+z2) 2 cos fi
Kąt zarysu	a,	tga, = tga/cos/S
Kąt zazębienia	(X(w	cos a m, = o cos a,/o„
Suma współczynników przesunięć		„ (^zi+^z2)(inva(w-inva,)
	^xz	2 tgo
Współczynnik przesunię-		Podział wielkości JCj; = jr,+-^r2
cia: - zębnika	X\	na składowe i x2 wykonuje się
- koła zębatego	*2	na podstawie tabl. 12.2.3, 12.2.4.

2. OBLICZANIE ODLEGŁOŚCI OSI a_w DLA ZADANYCH WSPÓŁCZYNNIKÓW PRZESUNIĘCIA A, i X₂ Tabl. 12.2.2

Suma współczynników		xz =x,+x2
przesunięć Kąt zarysu	a,	tga, = tga/cos/S
Kąt zazębienia	CXtw	inv aw= + inv a,
Odległość osi	O,	m (z,+z2) cos a, °^w~ 2 cos fi cosaw

min)

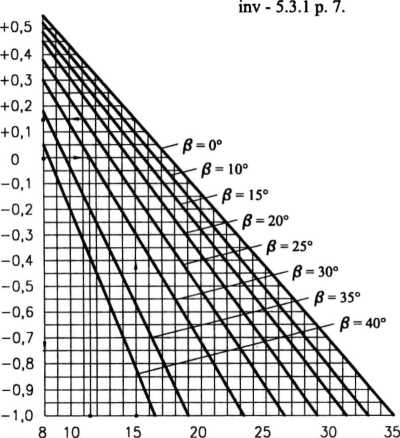
Rys. 12.2.1. Rysunek dla wyznaczenia x_mi

Przykłady. ^W zależności od Z i fi

1.    Zadane Z = 15; fi= 0°. Wyznaczamy X = 0,15.

2. Zadane X = 0; /?= 30°.    Wyznaczamy z min = 12.

3. WSPÓŁCZYNNIKI PRZESUNIĘCIA KÓŁ

Tabl. 12.2 3    ⁰ ZĘBACH PROSTYCH

Współczynnik przesunięcia zębnika koła zębatego *1 x2		Zastosowanie
0	0	Odległość osi aw jest zadana i równa	z, £21
+ 0,3	-0,3	aw=0,5m (z,+z2)	14$z,^20; 3,5
0	0	Odległość osi Ow	z{z 30
+ 0,5	+ 0,5	nie jest zadana	10$z,$30;

4. PODZIAŁ SUMY WSPÓŁCZYNNIKÓW PRZESUNIĘCIA X_t na X, i X₂

DLA PRZEKŁADNI O ZĘBACH PROSTYCH Tabl. 12.2.4

	Współczynnik przesunięcia zębnika koła zębatego *1 x2	Zastosowanie
0<*e<0,5	X M O	^zl^>zlmm^+2; ^z2^>21Z\ min Wg rys. 12.2.1 dla ■łT = *,= XE
0,5<Xe<1,0	+ 0,5 *1-0,5	Z,>11; Z2>Z2min+^2, z2 min wg rys. 12.2.1 dla x = x2 = xt - 0,5

1

ho=h'_a m +0,55-S_ntg (0,5 arc sin (5_fl tg²7'/d))=

=1-8 +0,55 • 12,195- tg(0,5 arcsin (12,195 tg²14°/64)) =

=8,154 mm.

("O    1»0)

2

NOMINALNY WYMIAR M PRZEZ WAŁECZKI Średnica wałeczków, mm D>l,67m.

Nominalny wymiar ślimaka przez wałeczki, mm

M=di-(pi-s‘m)cos7/tga+£»(l/ sina+1).

PRZYKŁAD 7. Ślimak o parametrach przykładu 6.

D> 1,67 m = 1,67-8 = 10,5 mm. Przymuje się D = 10,95 mm. M=di-(p,-s'm)cos7/tgar + D( 1/ sin ar+1) =

« 64-(n-8-l-8)cosl4°2'/tg 20°+10,95(l/sin20°+l) = 79,51 mm.