Str159 (2)

159

Tabl. 12.1.5. Dopuszczalne bicie promieniowe uzębienia F,

	Klasa dokładności
			6	n		7				8		_U_		9
Moduł	Średnica podziałowa d, mm
m,		>125	>400	>800		>125	>400	>800		>125	>400	>800		>125	>400	>800
ram	$125	$400	$800	$1600	$125	$400	$800	$1600	$125	$400	$800	<1600	<125	<400	<800	<1600
					Dopuszczalne bicie promieniowe uzębienia F,							/x m
l $m< 3,5	25	36	45	50	36	50	63	71	45	63	80	90	71	80	100	112
3,5$ m< 6,3	28	40	50	56	40	56	71	80	50	71	90	100	80	100	112	125
6,3$ m< 10	32	45	56	63	45	63	80	90	56	80	100	112	90	112	125	140
10 $ m < 16		50	63	71	—	71	90	100	—	90	112	125	—	125	160	160
16 $m<25	-		-	-	-	80	100	112		100	125	140		160	200	200

Tabl. 12.1.6. Tolerancja średniej długości pomiarowej T_win

Dopuszczalne bicie promieniowe uzębienia F_r, /un

0 0 ai«	•5* i^4'S 2 0 0	$8	>8 $10	>10 <12	>12 <16	>16 <20	>20 <25	>25 <32	>32 <40	>40 <50	>50 <60	>60 <80	>80 <100	>100 <125	>125 <160	>160 <200	>200 <250	>250 $320	>320 $400	>400 <500
						Tolerancja średniej długości pomiarowej Twm								, M^m
H,E	h	16	16	18	20	20	20	22	25	25	28	30	40	55	70	80	100	100	140	160
D	d	20	25	25	25	28	30	35	40	40	40	60	70	80	100	120	140	160	240	250
C	c	28	30	30	35	40	45	45	50	60	70	90	110	120	140	180	240	280	300	400
B	b	35	40	40	40	45	50	55	60	70	100	100	120	140	200	250	300	350	450	550
A	a	45	50	50	55	60	60	80	90	100	110	140	150	180	240	280	350	450	550	700
_	z	60	60	60	70	70	80	100	110	120	140	180	200	250	300	400	500	600	800	800
-	y	70	80	90	90	100	110	120	160	180	220	240	300	350	400	500	600	800	900	1100
-	X	90	100	100	110	120	140	160	180	220	250	300	350	400	550	700	800	1100	1200	1400

1.2. KOŁA O ZĘBACH SKOŚNYCH

Do obliczeń długości wzdłuż wspólnej normalnej zębów kół skośnych korzysta się z zależności i tablic jak do zębów prostych. Dla obliczeń korzysta się z ekwiwalentnej liczby zębów Zeq=zk, gdzie k=i(p) (tabl. 12.1.7).

Zwykle ekwiwalentna liczba zębów z_Cq nie jest liczbą całkowitą. Z tego powodu wprowadza się korektę długości wzdłuż wspólnej normalnej W_cą, mm, której wielkość jest zależna od (zcą-z^ą), gdzie z_eq jest całkowitą częścią ekwiwalentnej liczby zębów H'eq = 0,0149 (Zeq-Z^q).

Wtedy nominalna długość W_x wzdłuż wspólnej normalnej (dla a = 20°), mm

Wi = (W'+ Weq + 0,684 x) m.

Dalsze obliczenia wg p. 1.

PRZYKŁAD 2. Koło zębate z = 42, m - 5 mm, (i = 14°22', klasa dokładności 8-C, z = 0, zazębienie zewnętrzne (rys. 12.2.11). d=mz/cos 14°22' = 5 • 42/0,9687 = 216,78 mm; k = 1,0948 (tabl. 12.1.7); _Zcę=zi = 42 1,0948 = 45,98 (z^=45); Dla z^ = 45 Zw= 5 (tabl. 12.1.2); W '= 13,915 (tabl. 12.1.2); Wcg = 0,0149 (zeq z'cq) = 0,0149 (45,98 - 45) = 0,0146; lY_l = (lY+W_c?+0,684z)m = (13,915+0,015+0)-5 = 69,65 mm;

Tabl. 12.1.7. Wartości współczynnika k

do obliczeń ekwiwalentnej liczby zębów

P	k	P	k	P	k
8°	1,0288	13°	1,0768	18°	1,1536
8°20'	1,0309	13°20'	1,0810	18-20’	1,1598
8°40'	1,0333	13°40'	1,0853	18-40'	1,1665
9°	1,0359	14°	1,0896	19°	1,1730
9°20'	1,0388	14°20'	1,0943	19-20’	1,1797
9°40'	1,0415	14°40'	1,0991	19°40'	1,1866
10°	1,0446	15°	1,1039	20°	1,1936
10°20'	1,0477	15°20'	1,1088	20-20’	1,2010
10°40'	1,0508	15°40'	1,1139	20°40’	1,2084
11°	1,0543	16°	1,1192	21°	1,2160
11°20'	1,0577	16°20'	1,1244	21-20'	1,2239
11°40’	1,0613	16°40'	1,1300	21-40’	1,2319
12°	1,0652	17°	1,1358	22°	1,2401
12°20'	1,0688	17°20'	1,1415	22°20'	1,2485
12°40'	1,0728	17-40'	1,1475	22°40'	1,2570

Dla pośrednich p wartości k wyznacza się interpolacją. Dla p > 23° wartości k , wg [48].

Ewms= 0,100 mm (tabl. 12.1.3); F_r « 71 firn (tabl. 12.1.5); Ew_ms= 0,018 mm (tabl. 12.1.4);    7^ = 0,090 mm (tabl. 12.1.6);

Ewms=Eńms⁺Ewms = 0,100 + 0,018 = 0,118 mm;

W = (W_i-E_waa) -T_wm= (69,65-0,1 18)-o.m= 69,53.8,09 mm.

2. GRUBOŚĆ ZĘBA WZDŁUŻ STAŁEJ CIĘCIWY S_c I WYSOKOŚĆ POMIAROWA ZĘBA h_c

2a

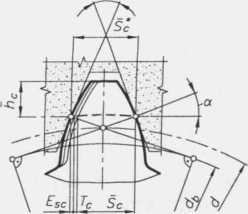
Rys. 12.1.3. Schemat pomiaru grubości zęba wzdłuż stałej cięciwy oraz odchyłki i tolerancje grubości zęba dla kół walcowych

1. Grubość zęba wzdłuż stałej cięciwy ( S_c) - długość cięciwy odpowiadająca grubości nominalnej zęba (rys. 12.1.3).

Grubość nominalna zęba wzdłuż stałej cięciwy, odpowiadająca nominalnemu położeniu zarysu odniesienia, mm 5_C= (1,387 + 0,643x)/n.

Rzeczywista grubość zęba wzdłuż stałej cięciwy (podawana na rysunku wykonawczym koła), mm Ś_c= (S_c -Ej_C)-T_c ,

gdzie E_Sc - najmniejsza odchyłka grubości zęba wzdłuż stałej cięciwy, mm Esc~ E_Hs 2 tg a — 0,728 /■)/,,