img043

x = 3 m; x = 5 m;

M_c = 10 kN • M,

15 • 2²

M, = 10--= -20 kN-m.

2

Wykres M, pokazano na rys. 3-24c.

Przykład 3-22. Wyznaczyć siły poprzeczne i momenty zginające w belce jednowspor-nikowej, obciążonej jak na rys. 3-25a.

Reakcje podpór wyznacza się z równań równowagi:

ZY=R_a + R_b-P = 0,

ZM_b= R_a-6-PS = 0.

Otrzymuje się:

R_a = 20 kN,    R_B = —5 kN.

Zwrot reakcji R_B jest przeciwny do założonego (rys. 3-25a).

Równania siły poprzecznej:

Vf^A = -P = -15 kN,

V^AB = -p+R_A = -15 + 20 = 5 kN.

Moment zginający określają zależności:

Mf* = -Px,

x = 0; M_c = 0, x = 2 m; M_a = — P-2 = — 30 kN-m,

M^AB= -Px + R_a(x-2),

x = 8 m; M_B =—15-8 + 20-6 = 0.

Wykres M_a pokazano na rys. 3-25c. Z wykresu tego widać, że rozciągane są górne włókna belki. Odkształcenie belki przedstawiono na rys. 3-25a linią przerywaną.

Przykład 3-23. Sporządzić wykresy V₂ i M₃ w belce jak na rys. 3-26a. Równania równowagi:

ZY= R_A + R_B — pll—P = 0,

ZM_a= -Pg-8 + P-6 + p-11-5,5 = 0.

Z równań tych otrzymuje się:

R_a = 54,1 kN,    P_B= 120,9 kN.

Równania siły poprzecznej:

Vf = R_A-px,

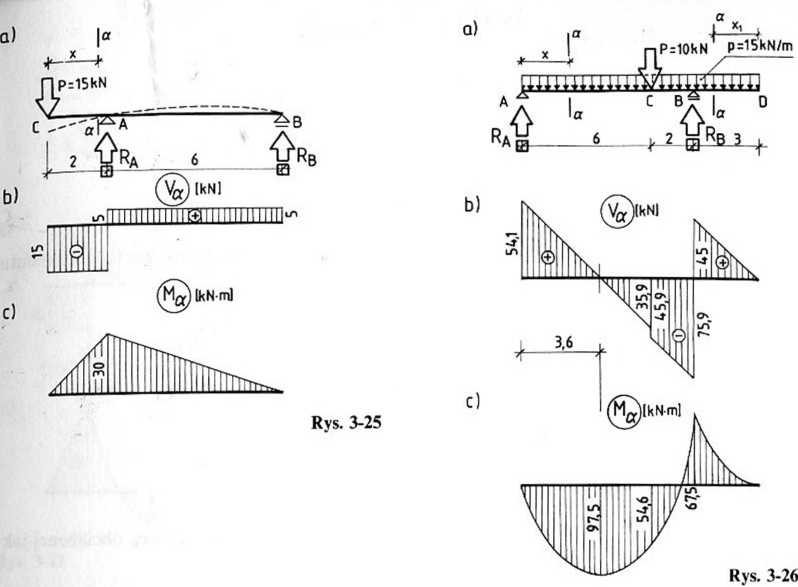
x = 0; V_a = R_a = 54,1 kN, x = 6 m; Vę = R_A—p-6 = 54,1 — 15-6 = —35,9 kN,

V™ = R_A-px-P,

x = 6 m;    F<? = 54,1-15-6-10 = -45,9 kN,

x = 8 m;    Fi = 54,1-15-8-10 =-75,9 kN,

V?^D = R_A-px-P+R_B,

x = 8 m; Vg = 54,1-15-8-10+120,9 = 45 kN, x=llm; V_D = 54,1 — 15-11 — 10+ 120,9 = 0. Wykres V_a pokazano na rys. 3-26b.

Równania momentu zginającego:

Mf = R_Ax-^-,

1 S • ^

x = 6 m; M_c = 54,1-6---= 54,6 kN-m,

c    ₂

= R_ax--~--P(x-6),

n t