img098 2

Największy moment zginający w belce swobodnie podpartej, obciążonej w sposób ciągły równomierny, nic może być większy niż M = 8,42 kN m. a więc

M_max = -- < M,

skąd

8M 8-8,42

p < -jr- = ₄ 52 = 3,33 kN/m.

Sprawdzenie największych naprężeń stycznych, gdy p = 3,33 kN/m:

V_max = 0,5pl = 0,5 • 3,33 ■ 4,5 = 7,49 kN,

bh³

12

12 -18³ 12

= 5832 cm⁴.

bh²    12-18²

S_x = —— = —-— = 486 cm³ (por. przykład 8-3),

O    O

V s

^rniax^,Jx

= 0,052 kN/cm² =

7,49-486

l_xb 5832-12 = 0,52 MPa < f_ivm = 1,4-1,0 = 1,4 MPa.

Z powyższych obliczeń wynika, że rozpatrywana belka spełnia wymagania stanów granicznych nośności, gdy wartość obliczeniowa jej obciążenia rozłożonego równomiernie p < < 3,33 kN/m.

Przykład 8-6. W stropie Kleina o rozpiętości w świetle ścian l_s = 5,30 m zastosowano belki stalowe dwuteowe o wysokości 220 mm, rozstawione co 1,50 m (rys. 8-11). Wartość obliczeniową obciążenia belki p = 13,83 kN/m określono w przykładzie 1-2. Sprawdzić, czy naprężenia normalne i styczne w przekrojach belki nie przekraczają odpowiednich wytrzymałości obliczeniowych. Belka wykonana jest ze stali St3S o wytrzymałości obliczeniowej = = 215 MPa.

Rys. 8-11

parametry charakteryzujące przekrój belki w postaci dwuteownika 220 mm (rys. 8-1 lb) są _fla_Stępujące (por. tabl. 14-24): l_x = 3060 cm⁴, W_x = 278 cm³, szerokość stopki s = 98 mm, grubość stopki t = 12,2 mm, grubość środnika g = 8,1 mm, promień zaokrąglenia między Rodnikiem a stopką r = 8,1 mm.

Określenie klasy przekroju (por. rys. 8-6):

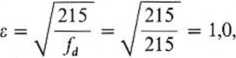
_ warunek dotyczący smukłości środnika

h — 2 (f + r) 9

220-2(12,2 + 8,1)

8,1

22,1 < 66e = 66,

- warunek dotyczący smukłości stopki

0,5(s — g) -r t

0,5(98-8,1)-8,1

12,2

= 3,0 < 9f. = 9,

- warunek smukłości przy ścinaniu (por. rys. 8-7)

h_

9

220

"IJ

= 27,2 < 70e = 70.

Przekrój zalicza się zatem do klasy 1.

Belka jest usztywniona w stropie. Dlatego przyjęto, że została ona zabezpieczona przed zwichrzeniem.

Największe wartości sił wewnętrznych w przekrojach belki (rys. 8-1 la):

Z = l,05/_s = 1,05-5,30 = 5,56 m,

V_max = 0,5pl = 0,5 • 13,83 ■ 5,56 = 38,5 kN,

M_max = 0,125pl² = 0,125-13,83 - 5,56² = 53,5 kN-m.

W przekroju, w którym moment zginający jest największy, siła poprzeczna jest równa zeru. Siła ta nie ma więc wpływu na nośność obliczeniową tego przekroju.

Sprawdzenie naprężeń normalnych (przekrój klasy 1) — wg wzoru (8-18); a_p = 1,07 dwuteownik zwykły

= 19,2 kN/cm² = 192 MPa < <xj_d = 1,07-215 = 230 MPa

5350

W_x 278

Sprawdzenie naprężeń stycznych — wg wzoru (8-20):

A_t. = hg = 22-0,81 = 17,82 cm² (por. rys. 8-7),

T = •

38,5

17,82

= 2,16 kN/cm² = 21,6 MPa < 0,58/_d = 0,58-215 = 124,7 MPa.

nr,- ^0t.^rzy^manych wyników widać, że przyjęta belka spełnia wymagania stanów granicznych

¹⁰sności.