img153 2

ROZDZIAŁ 7. PRZEKSZTAŁCENIE LINIOWE

ROZDZIAŁ 7. PRZEKSZTAŁCENIE LINIOWE

e) M\((p) ==

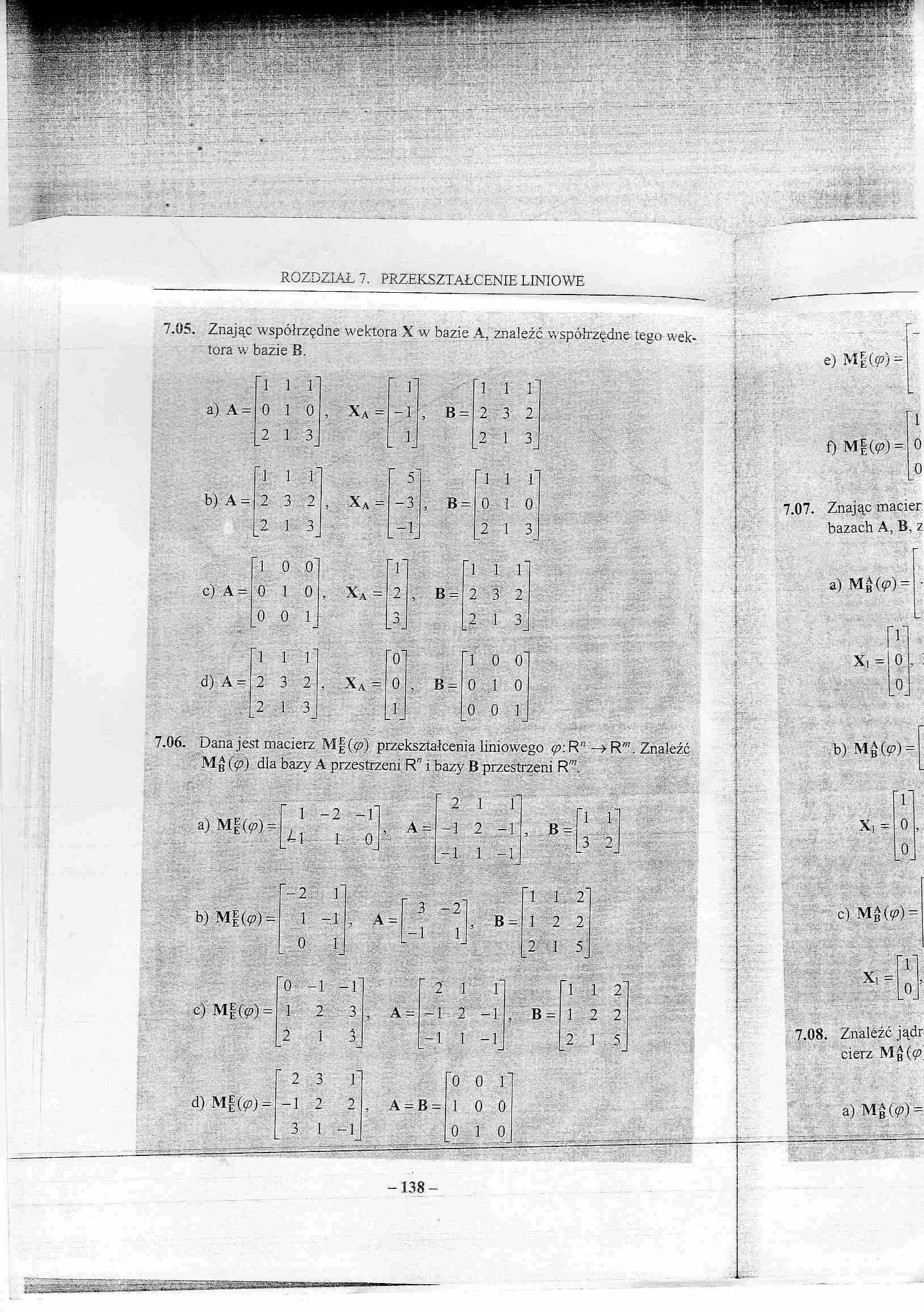
7.05. Znając współrzędne wektora X w bazie A, znaleźć współrzędne tego wektora w bazie B.

		"1	1	r
a)	A =	0	1	0	, XA =
		2	1	3	-
		'1	1	f	r
b);	A =	2	o J	2	, xA =
		2	1	3	-
		"1	0	0'	r
c)	A =	0	1	0	II X!
	. »| -	0	0	1	_
		"l	1	T	r
d)	A =	2	3	2	, XA =
		2	1	3

B =

1	1	1
2	3	2	I
2	1	3
'1	1	r
0	1	0
2	1	3	■

7.07. Znając macier bazach A, B. z

B =

	"]	i	r
, B =	2	3	2
-	2	1	o J
n	'l	0	0'
, B =	0	1	0
	0	0	1

a) M$($?)■=

X, =

L°a

7.06. Dana jest macierz M|(ę?) przekształcenia liniowego (p\R” -w R"’. Znaleźć Mg (<p) dla bazy A przestrzeni R'⁷ i bazy B przestrzeni R^w

a) MI(<p) =

ANANASA		2 1 f		>'^r' - Aj	■		T
1 -2 -f J-\ I 0	i A =	-1 2 -1	, B =	'i r _3 2_		x,=	0 o
. . .	•	-1 1 -1 -^1					_ -i

c)    =

b) Mg(p) =

2	r				"l	1	2"
1	-i		" 3 -2~			Ę&pź
		, A =	_-l 1.	, B =	1	2	2
0	i ^_	Ipi			2	1	5

A =

c) Mf (ę>) =

d)    =

0	-1	-1
1	2	3
2	1	3
' 2	n O	1
-1	2	2
o ć>	1	-1

A = B =

mm

' 2	1	r		"l	1	Z
-1 2		-i	i B =	1	. 2	2
-1	1	-i •• —		2	1	5

mm

0 0 1 1 0 0 0 1 o

Xi =

'1

A

7.08. Znaleźć jądr cierz M§(ć>

138 —