img251

Kinematyka ćwiczenia 2

Przykład 6

Pionowa winda przemieszcza się z położenia z = 0 w położenie z = 30 m. Pierwszy odcinek drogi równy h\ = 4 m, winda porusza się ze stałym przyspieszeniem a\, następny odcinek drogi pokonuje ze stałą prędkością V₂, zaś ostatnie trzy metry jest hamowana ze stałym opóźnieniem a₃. Należy wyznaczyć wartości liczbowe przyśpieszenia a\, opóźnienia a₃ i prędkości V₂ ruchu jednostajnego, jeżeli wiadomo, że czas jazdy windy jest równy t_c = 6 s oraz że dla z\ = 0, t = 0, V₀ = 0.

Przykład 7

Punkt poruszając się po linii prostej ze stałym przyśpieszeniem, przebywa kolejno drogi S\—1 m, s₂ =4 m w czasach t\ = 2 s i t₂ = 3 s. Wyznaczyć wartość liczbową przyśpieszenia a tego punktu.

Przykład 8

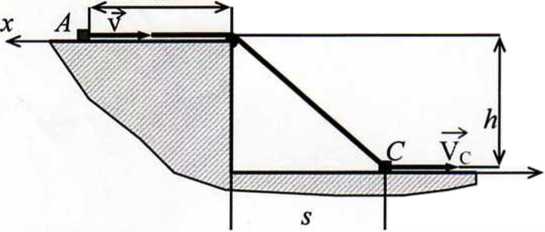
Do końca A nierozciągliwej liny AC przywiązane zostało ciało, które może ślizgać się po poziomej prowadnicy. Lina AC przerzucona została przez krążek B, który należy traktować jako punkt i jej koniec C ciągnięty jest z prędkością V_c = 3 m/s po poziomej prostej znajdującej się w odległości h = 1.2 m od prowadnicy (rys.8.1). Należy wyznaczyć prędkość punktu A w zależności od współrzędnej s (rys.8.1) oraz dla s = 2 m.

a:

B

s

Rys.8.1

Przykład 9

Na rysunku 9.1 przedstawiony jest schematycznie mechanizm korbowy składający się z wału korbowego OA, który może obracać się wokół osi O, korbowodu AB, oraz tłoka B. Końce korbowodu połączone są przegubowo z wałem korbowym i tłokiem. Należy wyznaczyć prędkość i przyspieszenie tłoka w przypadku gdy wał korbowy obraca się ze stałą prędkością kątową co czyli że <p = cot. Długość OA = r, długość AB = l (rys.9.1).