IMG 52

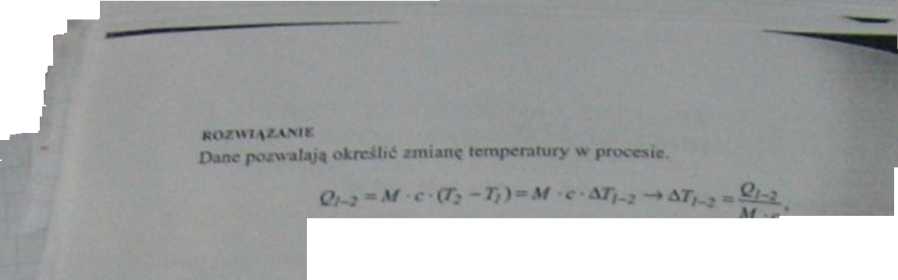
(i ( C)

Dla gazu doskonałego zmiana energii wewnętrznej i entalpii jest ftmkej^ _ly|_ko temperatury

du = e^i/T, di “ c_pdT..

Do wyznaczenia zmian tych wielkości musimy 2nałeżć ciepła właściwe przy stałej objętawi i ciśnieniu Ciepła właściwe gazu wyznaczymy, wykorzystując równanie Mayera i wykładnik izen tropy.

c_p -c_v = R, v = —, po rozwiązaniu tego układu równań mamy:

R

. c_v =518.2 J/(kg-K).

‘ K-l' 171

1.33-1

c_p = /? +c_v.

e_F =171 + 518,2. c,-689.2J/fkg-K).

Zmianę energii wewnętrznej obliczamy z równania: SU,_₂ = Mc„ (Ty - T, ) = Afc; AT,

SU_t_₂ = 5 518,2 • 149.7, AŁ/;_₂ = 3S7 872.7 J. AU,_₂ -387,9 Id.

Zmianę entalpii obliczamy z równania:

^/-z - Mc_p (T₂-T,) = Mc_p ST,

S/j_₂ =5 689.2 149.7, A/,_j =515866,2J. A/,_₂ =515,9 kJ.

Z pierwszej /osady termodynamiki wyliczamy pracę bczw zględną Q,-a - *^uh-» ♦    — *•/-* ^mQi-* ~ ^Aty#'²’

-114.7-387.9. L|., »-273.2 kJ.

Znak ..minus” przy wartości pracy oznacza, że praca została wykonana nad u Jem

Przykład 5.4

Obliczyć pracę bezwzględną i techniczną oraz ciepło wymieniane z otoczeniem 1/ • I kg gazu doskonałego, który rozpręża się od ciśnienia p_t “    •    •    ° *■

BU bezwzględnego, którego wysokość wynos, hj - 14901 mm. J _e - 13 545 kg en ) Objętość układu jest stała i wynosi V - 032 m . Ciepło przy stałym ciśnieniu wynosi c_f - 0.92 VJ/(kg K). a wykładnik izentropy K

ROZWIĄZANIE

Po przeliczeniu wysokości ciśnienia końcowego na jednostki układu SI z równa nu stanu wyznaczamy temperatury w stanach granicznych procesu.

Pz =P«_r 'g

/>, =13 545 9.81 1.490.    ^ =197 985.9 Pa,

U)

pk’ =    -»r = ^-

AfK

Indywidualną stalą gazową /? dla gazu wyznaczamy z równania Mayera “^c» -R (4.9a) i wykładnika izentropy K = —:

^ci-

R=c,

K-l

/? = 920    -¹. K = 262.86 J/(kgK).

7, = 426.08 K,

7; =

Temperatury wynoszą odpowiednio

3.5 10⁵ 0.32

1-262,86