KONSTRUKCJE STALOWE STR159

159

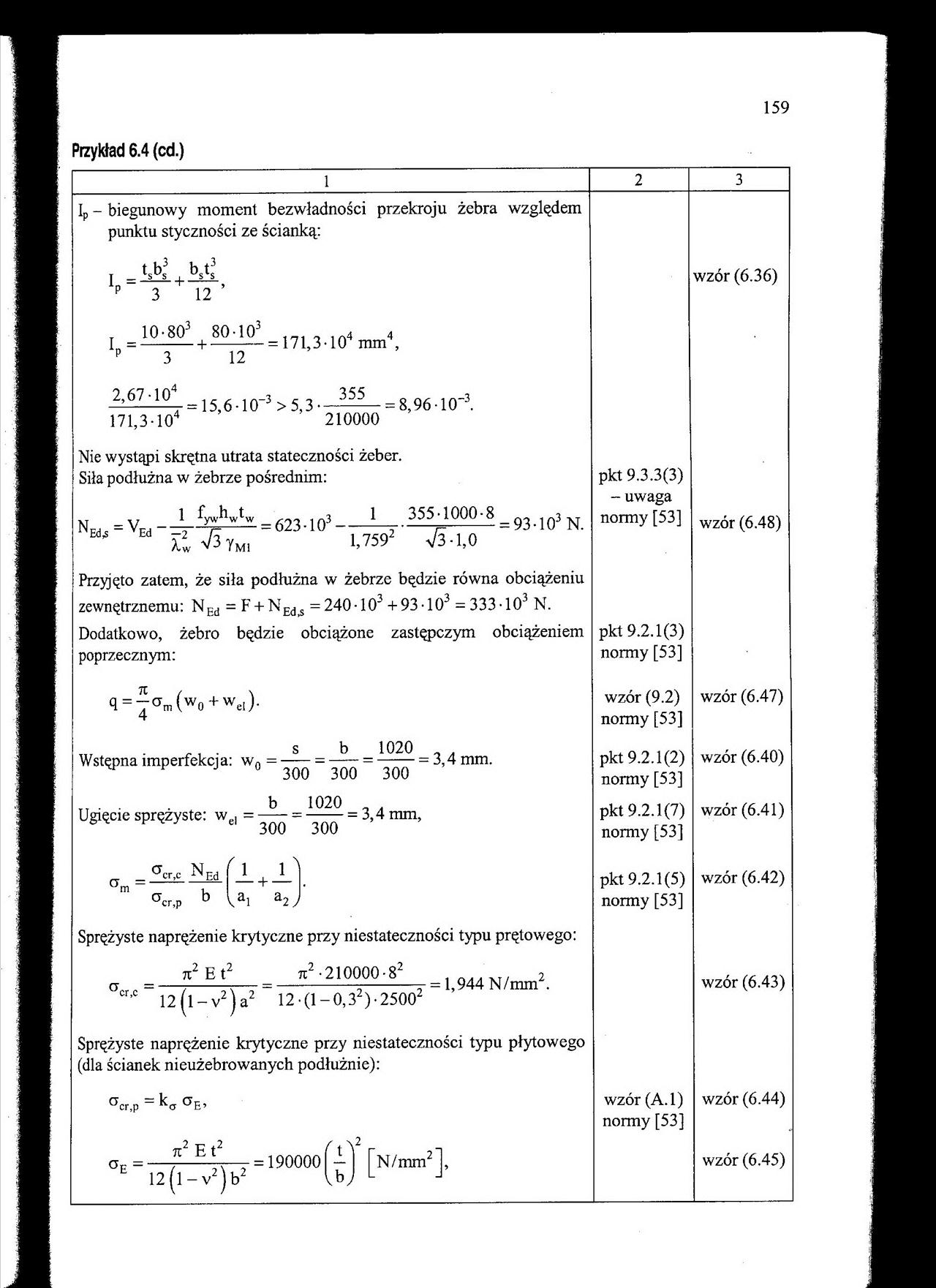
Przykład 6.4 (cd.)

I„-

biegunowy moment bezwładności przekroju żebra względem punktu styczności ze ścianką:

t ts^bs

I_n =--1-

^p 3    12

b_sts

_T 10-80³ , 80-10³ _łaiolA4_„₄ I —--l--— t/1,3*10 mm ,

^p 3    12

2,67_1°    ₆ iq-₃ -355_ o nr 1 n-3

I7l,3-l0⁴    210000

= 8,96 ■ 10 .

Nie wystąpi skrętna utrata stateczności żeber. Siła podłużna w żebrze pośrednim:

=    = 623-10¹

*3 Ym!

1    355-1000-8

1,759²    V3-l,0

Przyjęto zatem, że siła podłużna w żebrze będzie równa obciążeniu

zewnętrznemu: N_Ed = F +    = 240-10³ + 93• 10³ = 333• 10³ N.

Dodatkowo, żebro będzie obciążone zastępczym obciążeniem poprzecznym:

TC

^£ł⁼~^am(^W0 ^{+ W}cl)-

Wstępna imperfekcja: w₀ =

1020

300    300    300

= 3,4 mm.

Ugięcie sprężyste: w_el =

1020

^cr,c N_Ed

°cr,p b

el	300
	„ \
^r i	1 4_
^^ai	^a2 >

= 3,4 mm,

Sprężyste naprężenie krytyczne przy niestateczności typu prętowego: Tc² Et²    tc² •210000-8²

^CTcr,c -

12 (l - v²) a² 12-(l-0,3²)-2500^;

-1,944 N/mm .

Sprężyste naprężenie krytyczne przy niestateczności typu płytowego (dla ścianek nieużebrowanych podłużnie):

^cr.p    °E’

TC² E t

°E ⁼

12(l-v²)b^:

= 190000

V

0 [nWI.

= 93•10³N.

2	3
	wzór (6.36)
pkt 9.3.3(3) - uwaga normy [53]	wzór (6.48)
pkt 9.2.1(3) normy [53]
wzór (9.2) normy [53]	wzór (6.47)
pkt 9.2.1(2) normy [53]	wzór (6.40)
pkt 9.2.1(7) normy [53]	wzór (6.41)
pkt 9.2.1(5) normy [53]	wzór (6.42)
	wzór (6.43)
wzór (A.l) normy [53]	wzór (6.44) wzór (6.45)