Kotwica0026

52 4. Wymiarowanie elementów konstrukcji drewnianych

4.2.2. Ściskanie równoległe do włókien

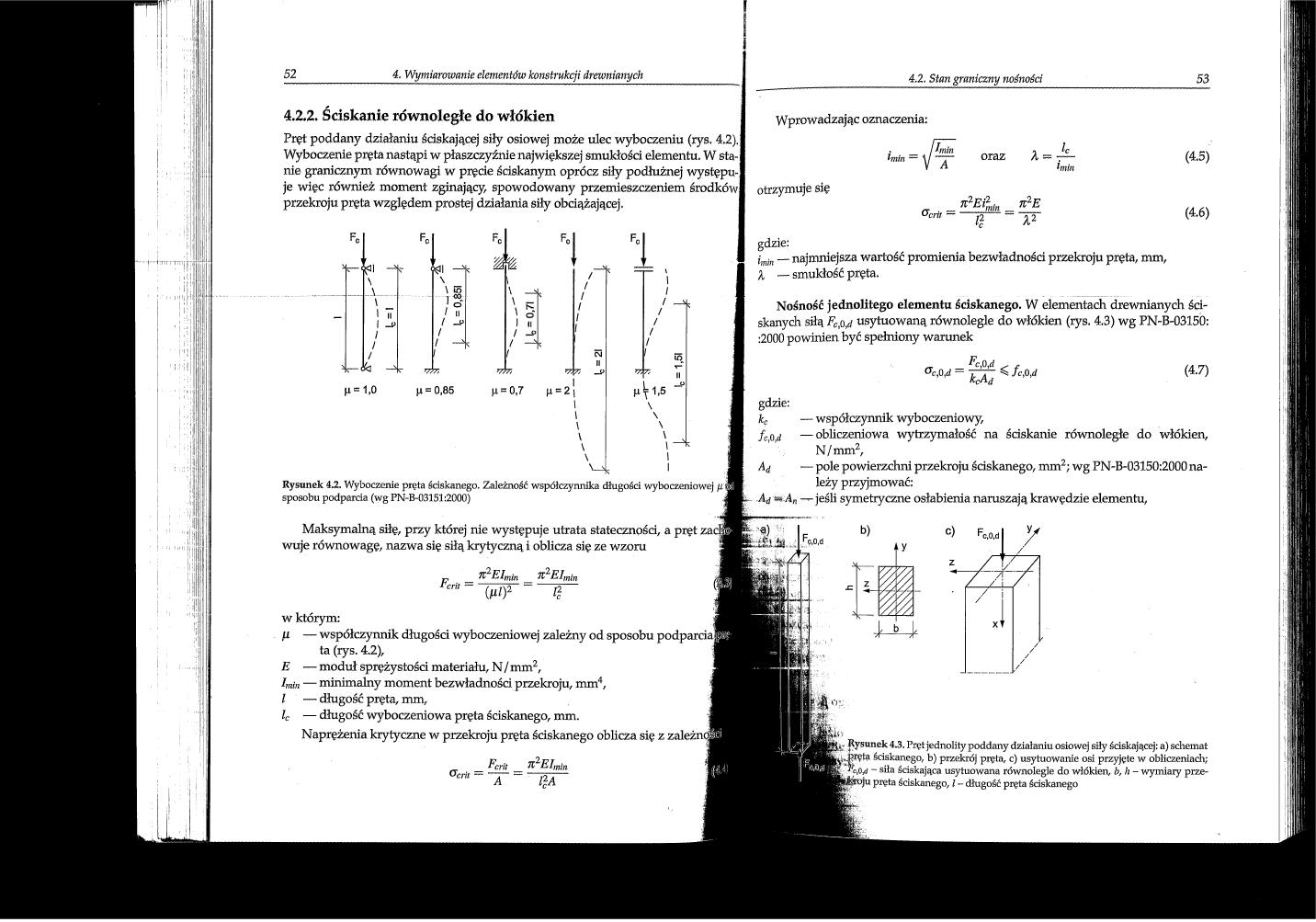
Pręt poddany działaniu ściskającej siły osiowej może ulec wyboczeniu (rys. 4.2). Wyboczenie pręta nastąpi w płaszczyźnie największej smukłości elementu. W stanie granicznym równowagi w pręcie ściskanym oprócz siły podłużnej występuje więc również moment zginający, spowodowany przemieszczeniem środków przekroju pręta względem prostej działania siły obciążającej.

e-fcai \

.A__

\

i Ti

I -V I I

/

y = 1.0

I

i n

/

/

i ~4

^r77r.

\x = 0,85

\ h: ° I n /

p = 0.7 M = 2 j

ćśł

H

1,5

Rysunek 42. Wyboczenie pręta ściskanego. Zależność współczyru\ika długości wyboczeniowej sposobu podparcia (wg PN-B-03151:2000)

Maksymalną siłę, przy której nie występuje utrata stateczności, a pręt zac wuje równowagę, nazwa się siłą krytyczną i oblicza się ze wzoru

Ferii —

FI_mi_n    7l^EI,„j_n

m²

%

w którym:

/i — współczynnik długości wyboczeniowej zależny od sposobu podparcia] ta (rys. 4.2),

E — moduł sprężystości materiału, N / mm², lmin — minimalny moment bezwładności przekroju, mm⁴, l — długość pręta, mm,

l_c — długość wyboczeniowa pręta ściskanego, mm.

Naprężenia krytyczne w przekroju pręta ściskanego oblicza się z zależne

Wprowadzając oznaczenia:

tmin —

/ hnin V A	. Ic oraz A = -— Imin	(4.5)
&crit —	n^2Eihn _ ą A2	(4.6)

otrzymuje się

gdzie:

i_mjn — najmniejsza wartość promienia bezwładności przekroju pręta, mm,

A — smukłość pręta.

-    _ ^Fcfl,d s ,

Gc,Q4 — ^    ^ Jcfi,d

Nośność jednolitego elementu ściskanego. W elementach drewnianych ściskanych siłą Fcfij usytuowaną równolegle do włókien (rys. 4.3) wg PN-B-03150: :2000 powinien być spehiiony warunek

gdzie:

k_c — współczynnik wyboczeniowy,

/c,<M    —obliczeniowa wytrzymałość na ściskanie równoległe do włókien,

N/mm²,

A_d    — pole powierzchni przekroju ściskanego, mm²; wg PN-B-03150:2000 na

leży przyjmować:

. A_d**A_n-~ jeśli symetryczne osłabienia naruszają krawędzie elementu,