Kolendowicz#9

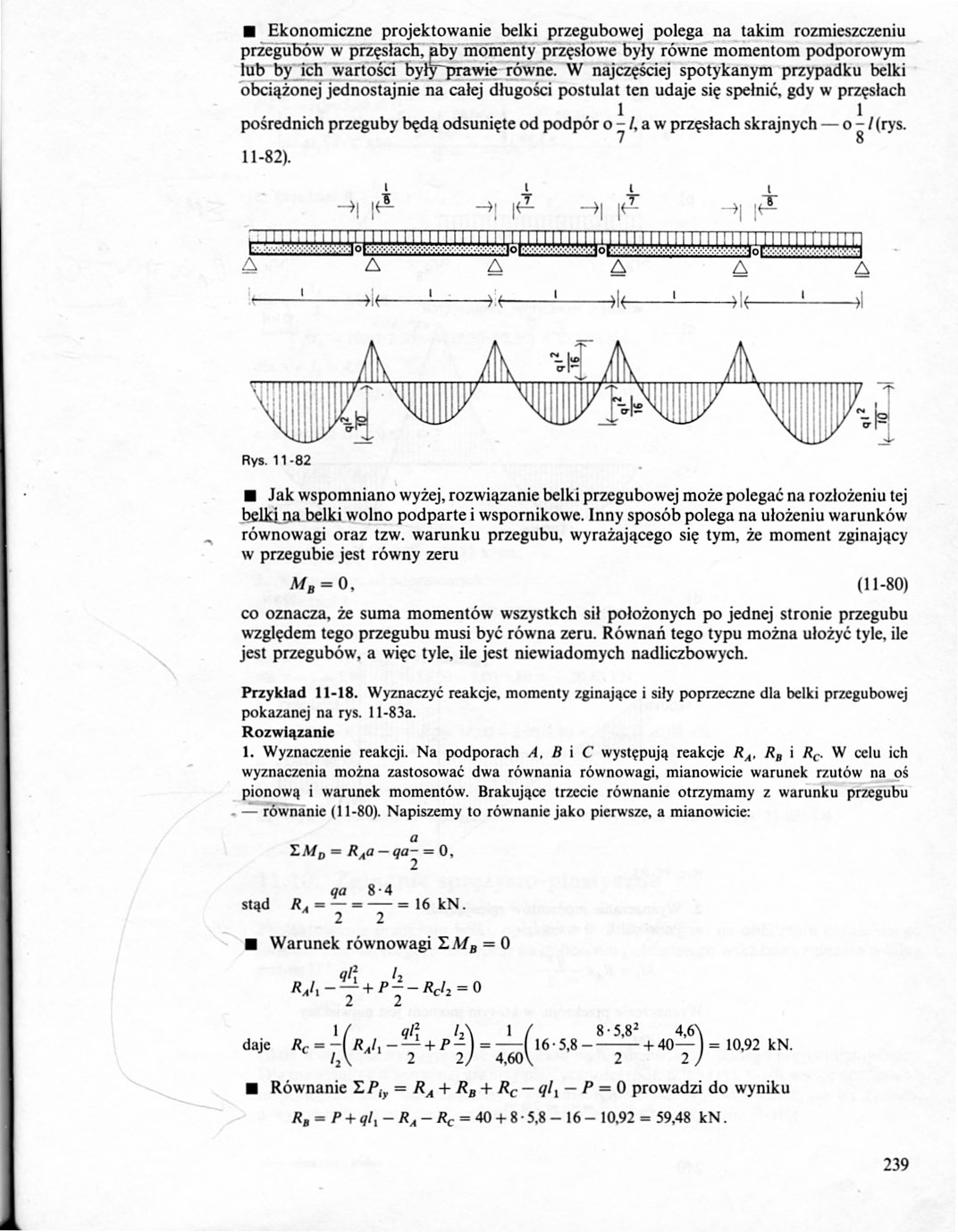
■ Ekonomiczne projektowanie belki przegubowej polega na takim rozmieszczeniu przegubów w przęsłach, aby momenty przęslowe były równe momentom podporowym lub by ich wartości były prawie równe. W najczęściej spotykanym przypadku belki obciążonej jednostajnie na całej długości postulat ten udaje się spełnić, gdy w przęsłach

, 1    1

pośrednich przeguby będą odsunięte od podpor o - /, a w przęsłach skrajnych — o - / (rys.

7    8

11-82).

->! i*¹    ~>| I*¹    ->|    ->|

A    A    A    A    A    A

•-¹-»i<-¹-i*-¹->k-¹-*k-¹->i

.

■    Jak wspomniano wyżej, rozwiązanie belki przegubowej może polegać na rozłożeniu tej belki na belki wolno podparte i wspornikowe. Inny sposób polega na ułożeniu warunków równowagi oraz tzw. warunku przegubu, wyrażającego się tym, że moment zginający w przegubie jest równy zeru

M_b = 0,    (11-80)

co oznacza, że suma momentów wszystkeh sił położonych po jednej stronie przegubu względem tego przegubu musi być równa zeru. Równań tego typu można ułożyć tyle, ile jest przegubów, a więc tyle, ile jest niewiadomych nadliczbowych.

Przykład 11-18. Wyznaczyć reakcje, momenty zginające i siły poprzeczne dla belki przegubowej pokazanej na rys. 1 l-83a.

Rozwiązanie

1. Wyznaczenie reakcji. Na podporach A. B i C występują reakcje R_A, R_B i R_c. W celu ich wyznaczenia można zastosować dwa równania równowagi, mianowicie warunek rzutów na oś pionową i warunek momentów. Brakujące trzecie równanie otrzymamy z warunku przegubu . — równanie (11-80). Napiszemy to równanie jako pierwsze, a mianowicie:

a

Z A/₀ = R_Aa — qa- = 0, qa 8-4

stąd R_a = — =-=16 kN.

2 2

■    Warunek równowagi Z M_B = 0

111]    l₂

R_aI.- — + P--R_cI₂ = 0 2    2

1/    ql*    l₂\    1 (    8 • 5,8²    4,6\

daje R_c = - R_Al,- — + P-) =- 16-5,8--+ 40— = 10,92 kN.

I₂\    2    2/    4,60V    2    2 )

U Równanie Z P_iy = R_A + R_B + R_c — ql_x — P = 0 prowadzi do wyniku

R„ = P + ql_l- R_A- R_c = 40 + 8• 5,8 — 16 — 10,92 = 59,48 kN.

239