Kolendowicz19

Widzimy, że wartości reakcji pionowych są takie same jak dla belki wolno podpartej. ■ Reakcję H można wyznaczyć obliczając moment zginający w dowolnym punkcie cięgna i przyrównując go do zera. Najwygodniej jest przyjąć najniższy punkt C cięgna, gdzie styczna do krzywej jest pozioma i siła wewnętrzna rozciągająca S jest również pozioma (rys. 15-10b). Z warunku równowagi rzutów na oś poziomą wynika wprost, że siła S = H. Wynik otrzymamy szybciej, jeśli zamiast względem punktu C obliczymy sumę momentów względem punktu A:

zma = 0,	ql l Hf — -— = 0, 2 4
stąd	^H = \1'	(15-29)
lub		(15-30)

gdzie M° = ę/²/8 jest momentem zginającym w środku rozpiętości belki o długości / i obciążonej tak jak cięgno.

■ Siła rozciągająca w dowolnym punkcie cięgna jest równa (rys. 15-11)

S =

H

cos)?’

(15-31)

gdzie fi jest kątem zawartym między styczną do krzywej przeprowadzoną w danym punkcie a prostą poziomą.

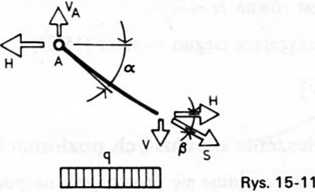
■ Największa siła rozciągająca występuje w miejscach zawieszenia cięgna i jest równa (rys. 15-11)

(15-32)

lub

H

cosa

(15-33)

■ Największe naprężenie w cięgnie

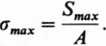
(15-34)

■    Wartość H i przy obciążeniu rozłożonym nierównomiernie oraz przy innych rodzajach obciążenia można otrzymać również za pomocą wzorów z p. 15.2.2.

■    Jeśli cięgno jest równocześnie obciążone równomiernie i siłami skupionymi, to reakcje pionowe obliczamy jak dla belki wolno podpartej, a reakcję H — ze wzoru (15-30). Na przykład dla cięgna pokazanego na rysunku 15-12 reakcje pionowe są równe

319