MATEMATYKA 1 2

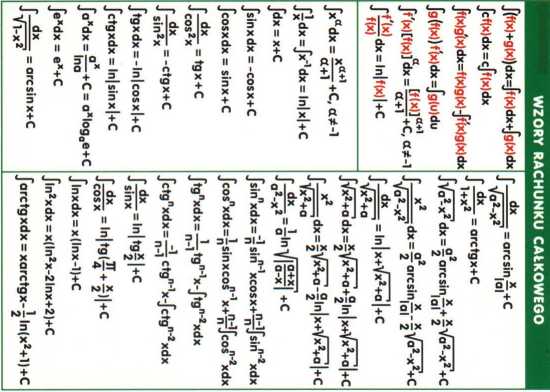
Równanie ogólne prostej 1 Ax+By+C = 0 Wektor n(A,B) jest prostopadły do prostej 1	PROSTA		Warunek równoległości i prostopadłości prostych li: Aix+Biy+Ci = 0 l2: A2X+B2y+C2 ^= 0 I3: y = mix+bi I4: y=m2x+b2 hll l2 <=^ a1b2-a2b1 = 0 hll2<=> a1a2+b,b2 = 0 I3IImi = m2 l3ll4<=> m2 = - — gdzie mi *0 i m2* 0 Jeśli % jest kqtem ostrym między prostymi li i l2 lub l3 i l4to: |A1B2-A2B1| | m1-m2 1
	Y y A	i
Równanie kierunkowe prostej 1 (nierównoległej do osi OY) y=mx+b gdzie m = tga m-współczynnik kierunkowy
	>a	^x X
Równanie odcinkowe prostej 1 (nierównoległej do obu osi) * + Y _ ■) gdzie a * 0 i b * 0 a b			Równanie dwusiecznych między prostymi li i l2 |A,x+B,y+Ci| |A2x+B2y+C2|
Równanie prostej przechodź, przez^punkt Pi(*i'yi)^1 prostopadłej do wektora n(A,B) A(x-x1)+B(y-ył) = 0			Odległość punktu P, (xvyi) od prostej Ax+By+ C=0 J |Ax,+By,+C| Va^2+b^2
Równanie prostej przechodź, przez punkt Pi(xi,yi) i o współczynniku kierunkowym m y-y-i = m(x-x1)			Odległość punktów P,(x,,y,| i P2(x2,y2) PiP2=V(x2-xi)^2+(y2-yi)^2 Środek odcinka P,P2 s( ^ ^^2)
			1 z y 2
Równanie prostej przechodź, przez różne punkty P^.y,) i P2(x2,y2) (y-yi)(x2-*i) = (x-*i)(y2-yi)			Pole tró|kqta o wierzchołkach P,(x„y,),P2(x2,y2) 1 P3(X3.y3l F = x1y2-x2y1+x2y3-x3y2+x3y1-x1y3|