skanuj0002

42

sta równoległa do prostej n jest prostopadła do a, a jej rzuty są prostopadłe do jedno-imiennych śladów płaszczyzny (rys. 2.37b).

42

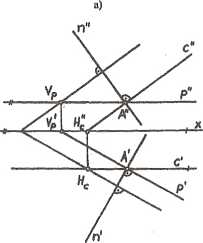
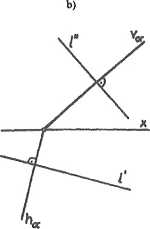
Rys. 2.37. Prosta prostopadła do płaszczyzny

2.9.5. DWIE PŁASZCZYZNY WZAJEMNIE PROSTOPADŁE

Jeżeli płaszczyzna zawiera prostą prostopadłą do pewnej płaszczyzny, to jest ona prostopadła do tej płaszczyzny. Inaczej, dwie płaszczyzny są prostopadłe, jeżeli jedna z nich zawiera prostą prostopadłą do drugiej płaszczyzny. Podane twierdzenia

a)    b)

Rys. 2.38. Dwie płaszczyzny wzajemnie prostopadłe

określają konstrukcje płaszczyzn wzajemnie prostopadłych. Pierwsza z nich polega na wykreśleniu rzutów prostej prostopadłej do danej płaszczyzny a («' x h_a, n" x vj, a następnie wyznaczeniu śladów płaszczyzny /?, zawierających ślady prostej prostopadłej n (rys. 2.38a). Druga konstrukcja przewiduje obranie na danej płaszczyźnie a prostej pomocniczej a, a następnie wykreślenie śladów płaszczyzny p (h₀ x a' i v_fi x a") (rys. 2.38b).

Zadanie 2.18. Znaleźć rzuty odcinka AP określającego odległość punktu A od danej płaszczyzny a (rys. 2.39).

Rys. 2.39. Dane do zadania 2.18

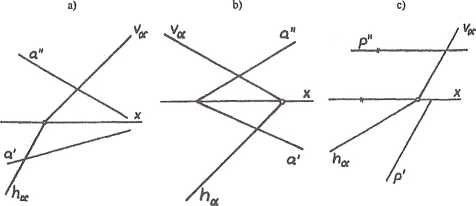
Rys. 2.40. Dane do zadania 2.19

Zadanie 2.19. Wyznaczyć rzuty kąta między prostą a i płaszczyzną a (rys. 2.40). Uwaga: Kąt między prostą a i płaszczyzną a jest zawarty w płaszczyźnie p prostopadłej do danej płaszczyzny a, przy czym a e p.

Zadanie 2.20. Wyznaczyć rzuty prostej n przebijającej trójkąt ABC (rys. 2.41) w środku ciężkości, przy czym:

a)    n - prosta dowolna,

b)    n - prosta prostopadła do płaszczyzny trójkąta ABC.