42323 img236

Równanie ogólne prostej:

ax + by + c = 0, gdzie a,b,ce R i co najmniej jeden ze współczynników a, b jest różny od zera.

-    wektor kierunkowy: s = (a; b),

-    wektor normalny: n =(-6;a),

-    kierunek prostej: k=—, b*0,k = tg<p,

b

-    równanie osi jc: _y = 0,

-    równanie prostej równoległej do osi x by + c = 0, b* 0,

-    równanie osi y: x = 0,

-    równanie prostej równoległej do osi y: ax + c = 0, a * 0.

-    przekształcenie postaci ogólnej prostej w postać kierunkową:

y = -—x - —    b* 0,

b b

-    przekształcenie postaci ogólnej prostej w postać odcinkową:

— +    = 1, p =    , q = —, a*0,ó*0,c#0.

-cc    ab

a b

	y
/<p) ' 0	s yS n \ -

yk

-H-

>'A    />

Równanie prostej przechodzącej przez dw a punkty /ł [a,;a₂],

S[ó,;6₂], (o, *6,):

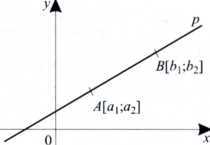
y-a₂ ó₂-a₂

x-a.

^b\~^a\

w postaci wyznacznika:

x y 1

а,    a, 1 =0.

б,    b₂

Rów nanie prostej w postaci normalnej

ax +by + c_ _ q _zna^ mianownika odwrotny niż znajduje się przy c. ±\/a² + b²