mech2 179

356

Rozwiązanie ogólne ma poBtać

u =    e^-wt + —^ cos u) t.

. 2ui

Stałe , C₂ wyznaczamy z warunków początkowych dla t = 0

	u |		1 ^	n j. p j.
		t=0		^G1 ^+C2 ^+ „ 2 " 2 tu
•	b I U		^n k
		t=0 “
stąd		^C1	II o PO II	OT ^2 ' 21 uj - g . ^2 ' 4 u)
Ostatecznie	"”72 4u)	[C^2i“^2	- e) Q	> + e-«^) + 2g

Zadanie 7 (rys. 268}

Tarcza kołowa o promieniu r obraca się dookoła pionowej osi ze stałą prędkością kątową u> . Do obwodu tarczy jest przymocowany na przegubie waloo-

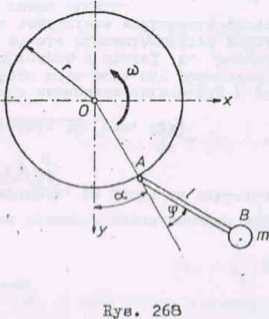
wym A nieważki pręt o długości 1 z umieszczoną na końcu masą m tak, że może wykonywać wahania w płaszczyźnie poziomej. Zbadać ruch pręta.

Odp. <p + ^JłL. eirup = 0,

T = 2 a

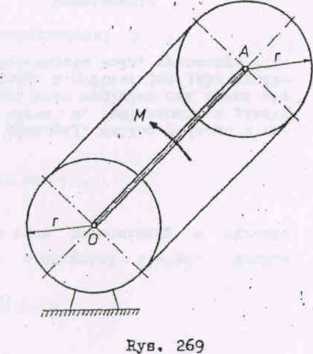
Zadanie 3 (jrye. 269)

Jednorodny pręt OA = 1 o ciężarze P może obracać się w płaszczyźnie poziomej wokół punktu 0. Rn koćcu A tego pręta osadzono obrotowo poziomy jednorodny krążek o ciężarze Q i promieniu r. Krążek ten połączono za pomocą nierozciągliwego wiotkiego pasa z drugim krążkiem, zamocowanym nieruchomo. Oś drugiego krążka ma kierunek-pionowy i przechodzi przez nieruchomy koniec pręta. Sa pręt OA działa moment M. Obliczyć przyspieszenie kątowe pręta.

Zadanie 9

stawionej w płaszczyźnie pionowej. Wyznaczyć ruch. punktu.

Punkt materialny porusza się pod wpływem siły ciężkości po cyklaidzie u-

A

o-

Q

ty

Rys. 270

Rozwiązanie (jrys. 270)

Równania parametryczne cykloidy mają postać:

z = c (a - sina), y =• c (jl - cosec).

Aby uniknąć zbyt skomplikowanych rachunków, jako parametr przyjmiemy nie ot ,lecz długość łuku cykloidy a, mierzoną od

wierzchołka cykloidy 0 do poruszającego się punktu.

W wierzchołku cykloidy 0 obieramy początek układu współrzędnych x',y\ równoległego do xy

Gdy y' = 0, wówczas 8 = 0, zaś a = n , stąd wyznaczamy etałą całkowania = 0, czyli

Energia kinetyczna punktu

Siła uogólniona:

.