mech2 18

•fcf

!M

l y_t

^podstawieniu otrzymanych wislkośol mamy zatem (jg!j Vg*«= 0,29 • 50,0 e 8,7 cm/e;    v_ę = 0,29 * 36,1 = 10,5 oa/a.

|lf®«ktar ~yZ ma kierunek prostopadły do odcinka CP_lp, a jego zwrot jest

jjjgggt CiS\i » u    -®-⁰

|«:»KOdny-‘* obrotem członu AB względeo ^?AB*

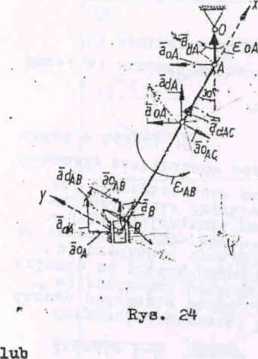
V2; Określenie przyspieszeń punktów (rys. 24).

Przyspieszenie punktu A składa się z przyspieszenia obrotowego i do-rŚaiowsgo

) v:

X

^loA

+ a

di.

^loA

OA

QA

2 • 10 = 20 cm/s ; -2

dA

OA

OA = 1,5

= 22,5 cm/s •

10

Wektor ma zwrot od A do 0. Wektor 'a^_A jest prostopadły do wektora ~a^ i ma zwrot zgodny z kierunkiem przyspieszenia kątowego

^ł0A*

Opierając się na wzorze określającym przyspieszenie punktu bryły w ruchu płaskim mamy

A

AB

^JAB

" _oA    ^VAB “AB

Przyspieszenie doosiowe punktu B względem punktu A

⁼    ^ ~ X ' ^0 ⁼ 5,00 cm

Wektor    ma zwrot od B do A, a wektor przyspieszeń i O obrotowego cT

jest prostopadły do niego.    .

Budujemy wielobok przyspieszeń wykorzystując to, że prosta ^yz^acząigCCI kierunek "ajj . jest znana.Z punktu B odkładamy kolejno wektory i.

które dają w sumie wektor a., oraz wektor a. (równoległy do członu Aft).

^A'    °AB

l

przez koniec wektora    prowadzimy prostą prostopadłą do AB.Punkt przecięcia tych prostych, wyznacza koniec wektora    W ten sposób wyzna

czyliśmy wektor a¹^_R. Wektor przyspieszenia a^ jest wektorem zamykającym wielobok. Opisaną konstrukcję zilustrowano na rys. 24.Zależność (1) możne zapisać w postaci analitycznej. Rzuty na osie x i y:

Hg COS	5°° = " ^aoA '	• cos 60° + Edjl •	cos 30° + a. ,	(2)
			^aAB
Eg COS	8 0 n » 0 >■	' COS 30° + ^adA ■	cos 60 - a„ °AB	(5)

Z równania (2) otrzymujemy

- a_oA cos 60° + a^_A cos }0^U + ^ad^jj ■^Sb "    cos 30°

= - ²⁰ ' ^ł₀fl_Ł| - ⁰'⁸⁶⁶    = 16,7 c»/_a².

W celu określenia przyspieszenia punktu C znajdziemy przyspieszenie kątowe członu AB. Z równania (3) otrzymujemy

a = a ®A3

eA

c®s 3® + ¹

dA .

ces &B^e =

= 20 • ©,®6G + 22,3 • ®,5 - 16,7 ¹ ®,5 = 2®,2 cm/s².

Wiadomo również, że przyspieszenie    można zapinać w postaci

a_c

^ao_A0 ^{F E}AB ' ^{Afl1 stf1d} ₍^B 'TT ~ ^ = °»3^{4 s}~²-

Kierunek przyspieszenia    względem bieguna A określa kierunek przy

spieszenia kątowego c _Ag. W danym przypadku ma ono zwret przeciwny do

AB¹

U)

Wektor przyspieszenia punktu C zapiszemy w poat&cit

w której

^JAC

= e

AB

AC s 0,54 • 20 = 6,0 cm/s¹ ;

'd_AC = "AB

AC

12

• 20 s 1,7 cm/s .

Wektor    jest prostopadły do wektora    i ma kierunek odpowiadający

przyspieszeniu kątowemu e^g.

. 'Przyspieszenie punktu C obliczamy wyznaczając rzuty:

^aCx = ^a1.- ^{+ a}HA ^C0S 30° - a,,¹ cos 60° =    .»

AC

MA

dA

11

1

^a~i +    + a„ + n.

C oA dA o_AC d_AC