mech2 49

4

J

I

i

9G

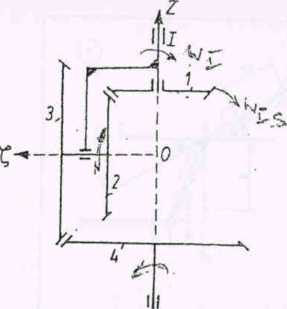
Dla kół 3 i 4

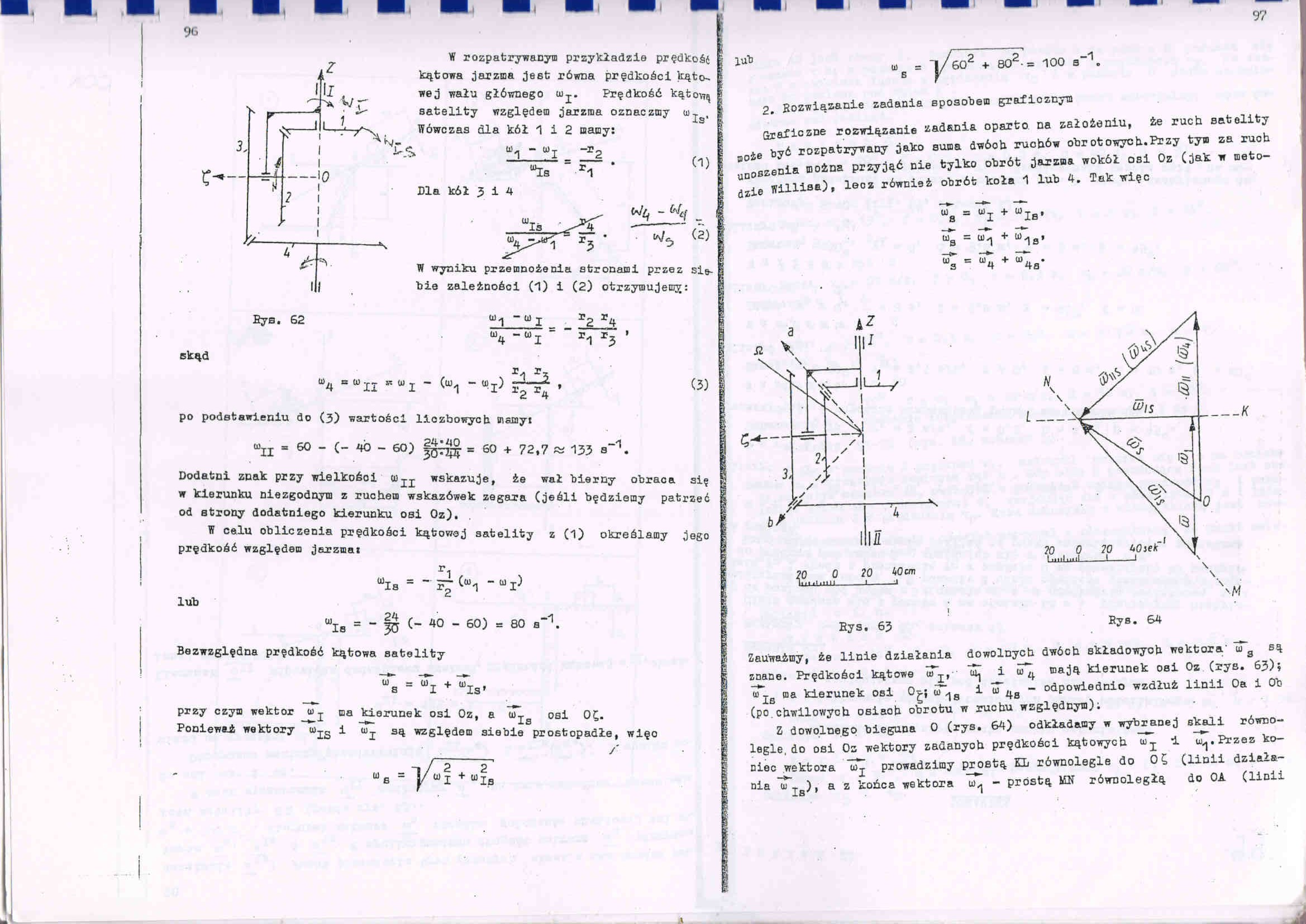
W rozpatrywanym przykładzie prędkośi kątowa jarzma jest równa prędkości kątowej wału głównego uij. Prędkość kątową satelity względem jarzma oznaczmy u>-_g. Wówczas dla kół 1 i 2 mamy: m* - U)_T

“la

CD

W wyniku przemnożenia stronami przez siebie zależności (1) i (2) otrzymujemy:

<d{,

- OJ,

_

^ (2)

Bys. 62

^r1 ^rJ

skąd

JP -C

“4 ^=WII ^B“I - ^(tu1 ““I^ Ą-Ą

(3)

po podstawieniu do (3) wartości liozbowych rnsmyt

“U - 60 - (- 40 - 60)    = 60 + 72,7 « 133 a~¹.

Dodatni znak przy wielkośoi Uijj wskazuje, że wał bierny obraca się w kierunku niezgodnym z ruchem wskazówek zegara (jeśli będziemy patrzeć od strony dodatniego kierunku osi Oz).

W celu obliczenia prędkości kątowej satelity z (1) określamy jego prędkość względem jarzmai

^r1

“t.    =    - — (u)„    - 0) _T)

'2

lub

²⁴ (- 40 - 60) = 80 a"¹.

Is = "

Bezwzględna prędkość kątowa satelity

“a = “i ⁺ “is*

przy czym wektor w j ma kierunek osi Oz, a u»_Is osi 0£. Ponieważ wektory    i tuj są względem siebie prostopadłe, więc

-Y

^wi⁺ “ia

2. Rozwiązanie zadania sposobem grafioznym

graficzne rozwiązanie zadania oparto na założeniu, że ruch satelity -oie być rozpatrywany jako suma dwóoh ruchów obr ot owych.Przy tym za ruoh _UDoszenia można przyjąć nie tylko obrót jarzma wokół osi Oz (jak w metodzie Willi⁰⁶), lecz również obrót koła 1 lub 4. Tak więc

“a = "I ^{+ u}Is<

^J1 ^T "la*

4a*

lub

-Y

60² + B0²-= 100 3^_1,

0).. + U) ,

Eys. 65

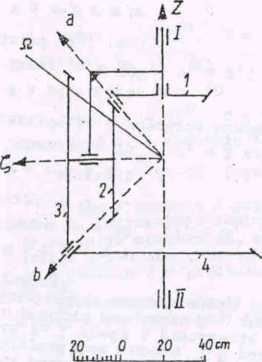
Zauważmy, że linie działania dowolnych dwóch składowych wektora' uT_s są znane. Prędkości kątowe uTp lUj i uT^ mają kierunek osi Oz (rys. 63);

ma kierunek osi 0^; uT^_g i aT^_g - odpowiednio wzdłuż linii Oa i Ob (po chwilowych osiaah obrotu w ruchu względnym);

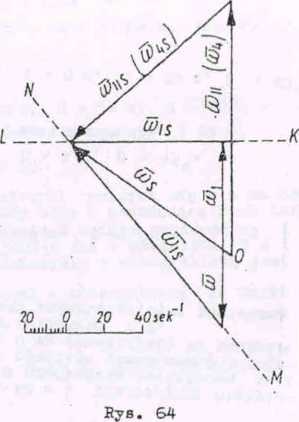
Z dowolnego bieguna O (rys. 64) odkładamy w wybranej skali równolegle, do osi Oz wektory zadanyoh prędkości kątowych    1    u^. Przez koniec wektora    prowadzimy prostą KL równolegle do 0£ (linii działa

ła mj_s), a z końca wektora u)^ - prostą MN równoległą do OA (linii