mechanika100

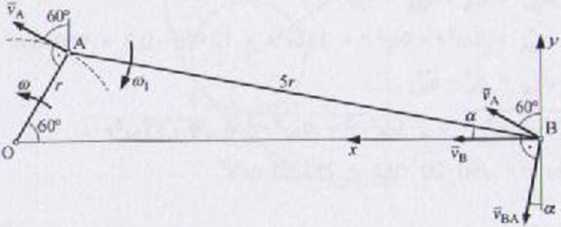
Wyznaczenie v_B, <■>,:

cor, Vba	= <*), *5r = 5u,r
^VA ^+ VBA *	ł ii »^tf

Z drugiego równania otrzymuje się prędkość kątowł* składowej obrotowej tarczy AB:

l_ur = lj97u,r •-?- =*<■>.= —-— w = 0,102-10 = 1,02 iwl/s 2 2^{V 1}    _v<97_r    ¹    ^97

Z pierwszego równania otrzymujemy:

_v. =^_cor*v^/3 _Lo>r=^|l +— Lr = 0,95(jr-0,95• 10 0,2 = 1,90 m/i

^B 2    2 _n/97    2 [ y97 J

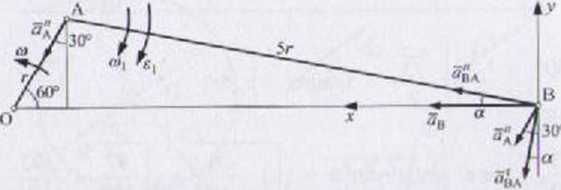
Wyznaczenie a_H. e, r. » u> =■ 0

200

Kinematyk* Kinematyka mechim/.mów plusk uh

H U^J<\    -    V⁵r 5c,r, o_B\ = ovSr = 5-^u²r = ^j<^^r

K ' «A * “ba ■ “A ^{+    +}    °E, * ^flB' ^aBv = ⁰

ii* sin 30° 4 n_BA sin a + <2_BA cos a - a_B

w_Acos30° - cos a + a^sina = 0

1,1- _v^,r3 5 ₂

fcrr* — + 5e,r*    +■—©v*JŁ— = a_R

2    ¹    10    97    10 ^B

, ^3    .    t/§7    5    ₂ /3 _n

«.» r--i— - 5e./*• -- + W7^,jl -0

2    ¹    10    97    10

/ •initfiego równania wyznaczamy przyspieszenie kątowe składowej obrotowej li.iwy AB:

97

, l©²-_v/97e, + ^?©² = 0

z*'', -    l^⁹⁷

^|l    |a>²« -0,17o²= -0,17-10² = -17 rad/s² (opóźnienie kątowe)

■ pierwszego równania otrzymuje się:

I*..    * o>⁷r - 3(J(-O_ł17G)²)r + —*—co²r = -- -^•0,17 + —-—)(o^:r =

*    2    2    2_v^7    \2    2    2 y§7

• 0,40©V = 0,40 10²- 0,2 = 8 m/s²

/ nianie 2.23

r*|))iin jest mechanizm korbowo-wodzikowy. Korba C)A jest w ruchu jednostajni' przyspieszonym. Przyspieszenie kątowe e ■ const. W chwili t - 0 korba 0\ jest nieruchoma. Wyznaczyć prędkość i przyspieszenie punktu B w chwi-D«“< i konfiguracji układu, Zastosować metodę superpozycji.

v» sin 60° * v_BA sin a v,

B

v_A cos 60^a - v_QA cos a = 0

air

.£.₅<o_ir£._VB

2 ¹ 10 ^B

- 5c»),r* ^v— = 0

Hltiiii c, r, / - 4r. o>(0)»0, «p(f_l) = 30°

•".l ane: V_B,

brnifliyka. 2.2.4. Kinematyka mochuntzmów ptokich

201