mechanika108

Obliczenia dla przykładowych danych:

Kir)

U = 6,28 —, b « 0,4 m

s

- & -6,28^ ♦ I *6,28e. = 5,44i_v ♦ 3,14i_i

<a = —■-6,28e_v » ~ •62&e_z = 5,44e_y + 9,42e.

e- y ^{6,283 =} "³⁴>¹⁵®*

rad

s²

5 ♦ £,

rad

s

rad

s

Vg ⁼ “-6,28 0,4e, - ³ -6,28 0,4e, + ^ -6,280,4e, = 1,88?, - l,88e_v ♦ l,09e. 4    4    ⁷    4

a„ = | • 6,28= ■ 0.4?, + | ■ 6,28' • 0.4 ?_y - 2.1.66?, • 1 l,83e,

Zadanie 2.29

Stożek toczy się bez poślizgu po płaskiej powierzchni. Okres precesji wynmi 7^, a wysokość stożka wynosi h. Wyznaczyć wektory to. e, v_B. a_B w cłl\M lowej konfiguracji układu.

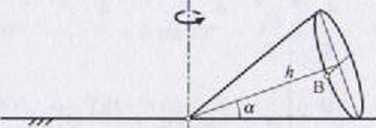
Dane: 7*₊, h

Rozwiązanie

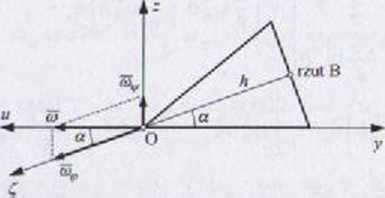
Stożek jesl w ruchu kulistym typu precesja regularna. Kąt nutacji wynon 90° + a. Prędkość kątowa obrotu własnego pokrywa się z osią stożku Wektor chwilowej prędkości kątowej <u jest poziomy, o zwrocie w lewo.

216

Kinematyka 2.2.5 Precesja regularna tiulu sztywncia*

ści geometryczne:

m.

cosa		b- ^h
		cosa
Iga	«=>	c = A tg a
sina		J = A sin a
cosa	-	e = A cos a
OB =	cex	+ eev + des =
2:t ’^T,

lYy znaczenie wektorów w, e, Vg, a_Q:

sina

sina

,o    ^wt

cos a ==> w = co cos a = —— cos a = w ctga

■    sina

W- " -w^cosa-e. - to sina-e,

*    y <*

-» - w ^ ctg a • e_v - w^-e_Ł m ■ -we. = -w_ftctga*e_y

—— cos a -e_v - -7-^ sina e.

sina

sina

I • «_txo_f ^s

0

w.

0 -w^ctga -w^

IV ' »' = uxr =

- w‘ ctga *e_t

^C*    ^ey    ^et

0 -w^ctga 0 A tg a A cos a A sin a

■    , cosa _

= I -w^ A-sin

sin a

ina je_t

L

(w .A—!—Iga Ie, =    w, A cos a e_r + w. A-e,

♦ tga J ‘    *

kliK-fttaiyk.i 2 2 5. Precesja regularna dala sztywnego

2I7