mechanika112

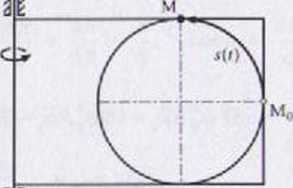
wym jednostajnym, z prędkością kątową u> = const. Wyznaczyć prędko *5 i przyspieszenie punktu M w chwilowej konfiguracji układu.

S.

I-fe—ł—+ * I

U

Dane: b - 0,2 m

v, =■ 1 m/s o = 20 rad/s

Rozwiązanie

Wykorzystujemy wzory (2.69).

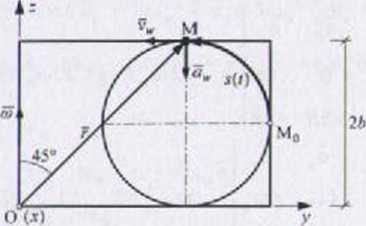
Punkt M jest w ruchu złożonym. Ruch unoszenia jest ruchem jednostajnym, obrotowym wokół osi pionowej. Ruch względny jest ruchem jednostajnym okręgu, przy czym w chwili początkowej punkt jest w położeniu M₀. Pot/u tek układu odniesienia xyz należy przyjąć na osi obrotu tarczy.

€ = (O « 0

r = 2 6e_y + 2 be_z,    r =

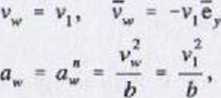
w = oe

y[2bf + {2b)‘ = 2 \j2b

^w * b ¹

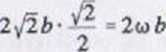
v_g ■ v_uC_ł = lube.

v_u = w x r, v_u = cir sin45° = <a

V - V_M = V, * v„ = -2(o 6e_f - v,e_r

224

Kinematyko. 2.2.6 Kinematyka punktu muicnalnctfo w ruchu /In/i-nt

-    ^(-2+(-v,)² = finty * v? = v4 • 20²• 0,2² ♦ l² = 8,06 m/s

-    c x r = 0

u xv_M, a* ■ wt^sinęO⁰ = o)-2w/>l = 2o²6 • -0"^ = -2 <o²6e_v

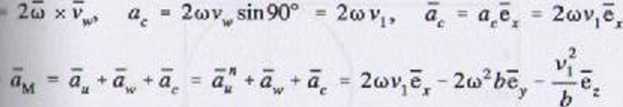
2

2

^por.f .(-20²*)²*

=    4ui²v,² - 4(o*b²

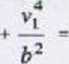
V,

b) \

4 * 20² 1² M-20⁴ 0^² + — = ^7225 - 165 m/s²

N    0.2²

m/wiązaniu wykorzystano definicję iloczynu wektorowego, zgodnie z któ-" flor wynikowy ma zwrot zgodny z regułą prawej dłoni. Zauważmy, że /cnie v_a byłoby łatwiejsze, jeśli punkt O zostałby przyjęty w górnym viii rogu tarczy.

lunie 2.33

uh materialny M porusza się po okręgu wpisanym w tarczę prostokątną. »m h punktu M jest jednostajnie przyspieszony, przy czym przyspieszenie I7IIC wynosi a_r W chwili r = 0 punkt jest nieruchomy w położeniu M₀ i m jest w ruchu obrotowym jednostajnie przyspieszonym, przy czym przy-fs/uiie kątowe wynosi e. W chwili t ■ 0 tarcza jest nieruchoma. Wyzna*

< prędkość i przyspieszenie punktu M w chwilowej konfiguracji układu, lir    .*

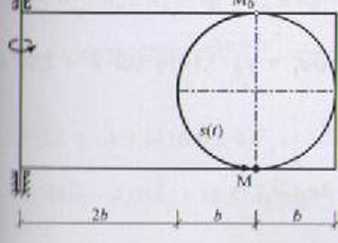
Dane: b - 0,2 m

n, = 2 m/s² c = 4 rad/s²

225

miiInLi 2.2 A Kinematyka punktu matorminogo w mchu /.łożonym