mechanika135

(1)    =* t = - {X b)

c

(2)

A sin

1

cj-(* - b) c

. . ( o ab]

*^sinh*’Tj

m

Tor ruchu jesi sinusoidą o amplitudzie k i długości lali k wyznaczonej z warunku:

"x = 2* -*■ X - ^ c    w

Przemieszczenia początkowe:

x₀ = x(0) -    = 0,2 m. y₀ - y(P) = *sinO = 0

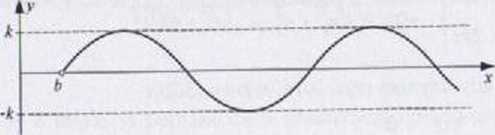
Wyznaczenie wektorów v{/), /*{*)’• v_r(/) = i(f) = c - 2 m/s

v_y(r} = j>(/) = £u>cosid/ = 0,l *20 cos 20/ = 2cos20r P_x(t) = mx(t) = 0

p^(l) = my(t) * mv_y(0 = -mA:<a²sin«d/ = - 10 0,1 *20“sin20/ = -400sin20/ P(t) = (-400 sin20/)e_y [N]

Prędkości początkowe:

Xq = ^v’x(°) ^{= 2} “fo >0 ⁼ vy(°) ⁼ *^{wcos0 =    =} °‘¹²⁰ = ² mis

v(r) = 2e_t + 2cos20/e_v [m/s|

Zadanie 3.3

Punkt materialny o masie m porusza się po okręgu poziomym o promieniu r_Q, przy czym współrzędna torowa (krzywoliniowa) wynosi:

s{/) = b +cr +

Wyznaczyć siłę PU) wywołującą ten ruch oraz wartość tej siły w chwili / » 5 s. Przyjąć: m = 2 kg. r₀ = 0,3 m, ó = 0,1 m. c = 0,2 mb, e = 0,3 m/s\

270

lozwinzanie :hemat obliczeniowy:

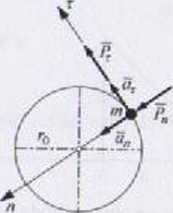
<kłodowe siły czynnej />(/) we współrzędnych naturalnych wynoszą (wzory (3.4)): P.ir) = mś(r)

*'^f) = ^mi

!(/) 3

p(0

gdzie:

itr) = c - 3et², S(t) -- bet, pif) = _r

IM =»■ P_t(r) = 6met = 6 0,2 0,3-f = 3,6f [N]

1(2) => P.(t) = ^m‘- ’-^{3U    2}

'o

o)

(2)

/>.(/) - "(e -3er³)² - A -(0,2 • 3 0,3f²F = 6,67-|0,2 + 0,9r³)² [N|

>'» ' fólt) * Pl(t)

jf,|5) - 3,6-5 = 18 N, P.(5) - 6,67-(0.2 ^0,9-S³)² = 3437 N ł(J) -    -> 3437² * 3437 N

/ ulanie 3.4

f*iuiki materialny o masie m = 10 kg porusza się po prostej poziomej pod opływem siły

|2r, 0 < / s 3 s [N] 1 0.    / > 3 s

f'^/v warunkach początkowych *(0) = 0, *{0) = 0. Napisać równanie ruchu 11 ofcwiązać je.

Li'-

Dyuamik.i V2 I Dynamika punktu matcnnlncgu be/ *nvt »    -kil. Dynamika punktu materiaIncgo be/ więzów

271