mechanika166

3.2.4. DYNAMIKA CIAŁA SZTYWNEGO W RUCHU OBROTOWYM

Zadanie 3.37

Prostopadłościan jednorodny ścięty, o masie m, obraca się wokół osi pionowej z prędkością ca = const. Wyznaczyć reakcje dynamiczne w łożyskach obrotowych bryły, w chwilowej konfiguracji układu.

A

O

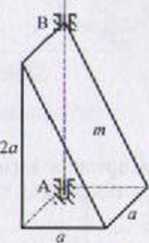
Dane: m - 100 kg a = 0,2 m (*) = 50 rad/s Szukane: R_K

B

R

Rozwiązanie

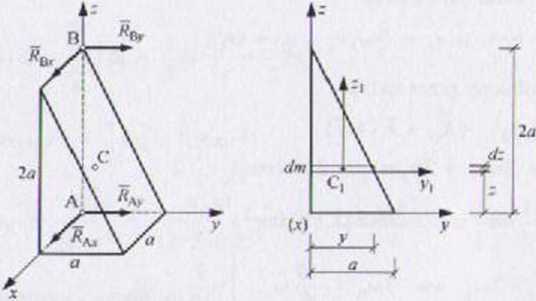
Bryła jest w ruchu obrotowym jednostajnym (co = const. e = 0). Należy wyznaczyć następujące charakterystyki geometryczno-masowe: b. c, jc_c, y_c. D_tz, D_n (rys. 3.19, wzory (3.81)). Początek układu xyz można przyjąć w punkcie A .Schemat obliczeniowy ma postać:

b = 0. c - 2a

332

Dynamika. 3.2.4 Dynamika ciała K/iywnc^o w ruchu obrotowym

tl    t,C,

Ta

cLD_ = dZ>._ ♦ dtn ■ x_r z- - 0 + — y dz • ■- z - — zy dz ^c'~    _a²    2 In ’

k. ■/*“»«■ 5/*(-^dł-Ś/(«'M^d* ⁼

nur

3

2^12 6

Układ równań ruchu obrotowego bryły (rys. 3.19b, wzory (3.107)):

^r^*^rh. =    (»

* «Bv * »(    ⁺ **c)    (2)

*a,* *n/ ’    (3)

^rk,I>-^rh.‘^: “    -O_k'    (4)

333

Współrzędne środka masy C (symetria bryły, środek masy trójkąta):

1 1

*c ³ 2°' ^yc = 3°

Wyznaczenie masy różniczkowej dm (wykorzystanie twierdzenia Talesa):

-a a 2a 2

m m

p = — = —

V

a

2a    2a - z

1

° ’ 2^Z

m

dm - p d^ = ‘fl-ydz = — vdz a³    a⁷’

Wyznaczenie momentów' dewiacji: dD * dZ> +dm7_cz_c = 0 ♦ -^ydz ■    = ~^~zy²dz

yz    Z:-i    ‘-iM    _n2    9_    -)„2 ^x

la    la

2 2a

Ta

■ ś(i*^v "5“’ * tHC• śK    ^

az² ♦ -z³ ldz ■

Dynamika 3.2 a Dynamika ciała sztywnego w ruchu obrotowym