mechanika18

(163)

Wypadkową obliczamy ze w zorów-:

* • E ^pi ’ ^WŚ. * ^ł "A

I-I

^w, - e^pu- i%. ",‘i\

M    1-1    1-1

Przestrzenny /.bieżny układ sił jest w równowadze, jeśli W » 0, tzn

^ - 0 — E^ = o

i-i

(1.64)

% - o -

i-J

* = 0 — £ - ° i-i

W praktyce stosujemy zapis symboliczny trzech równań równowagi statycznej (3RRS):

£^r"°. £z 0    (1.65)

2. Przestrzenny równoległy układ sil

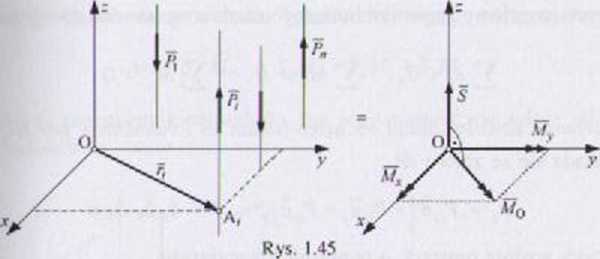
Rozpatrujemy zbiór sił równoległych do osi Redukując ten układ do punktu O, otrzymujemy siłę ogólna S i moment ogólny M₀. określone wzorami (rys. 1.45):

ś ■ E ^pi⁵z * ^sś<

l-l

*« * E^p*

l-l

"o" E^x p, E

i-i

l-l

e    e    e

■r y    z

^XA, >A, 0 0    0 P..

(1.66)

- Ei^a,)

i-i

", ■ E(-V_aJ

36

Stntyku Podstawy teoretyczne

Wynik S, jest pośrednim wynikiem redukcji. Jeśli S * 0, M_Q # 0, to nut/na znaleźć taki biegun redukcji A(x_a, y_A, 0), ze układ redukuje się tylko d" siły ogólnej zwanej wypadkowy W (rys. 1.46). Aby wyznaczyć odległość punktu lokacyjnego prostej działania wypadkowej od punktu O. redukujemy pm/ukiwaną wypadkowi} do punktu O:

S = W => W = W,e_t> W. = S_t

(1.67)

A#_n = Wa - Sa -» a = — = ^M-

°    5 |S_r|

K(imię a należy tak odłożyć, aby otrzymać w-łaściwy zwrot momentu M_Q.

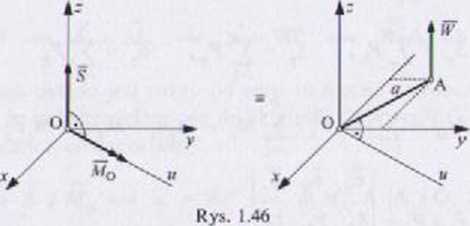
Jrśli S = 0, M₀ * 0, to układ redukuje się do pary sił o momencie M = M_n. Przestrzenny równoległy układ sił jest w równowadze, jeśli S = 0.

M_n = 5. tzn.

S.-0 - o

i-l

", - o — E(Va,) ■ ⁰    <>•«>

", - o -* E(-Va,) = o

I-I

37

Si.nyka 1'ikUuwy teoretyczne