mechanika39

(3) =>    0,5591 = G • 0,447/♦ 2G* 0,894/ |:/

0,559R_b = 2.235G ;:0,559,    « 3,998G = 4G

(|) => H_A = R₀sina = 4G-0.447 - 1,788G

(2) => K_a = /^cosa 3G - 4G-0.894 - 3G = 0,576G

^Rk ^s \j^Hi* ^Vl “    88G)² + (0.576G}² « l,878G

Odp.: //_A - 1.788C,    - 0.576G. /?_H = 4G.

Zadanie 1.27

Blok o ciężarze 3Q jest oparły przegubowo na podłożu i swobodnie na belce w miejscu wyokrąglonej krawędzi. Belka o ciężarze Q jesi zawieszona prze gubowo na ścianie pionowej i opiera się swobodnie wyokrąglonym końcem na powierzchni poziomej. Geometrię układu podano na rysunku. Przyjąć schemat statyczny układu i wyznaczyć reakcje. Blok i belka są jednorodnymi ciałami sztywnymi.

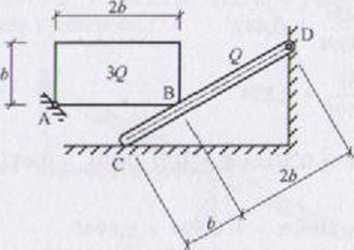
Roz.wuizanie

Blok o ciężarze 3Q naciska na belkę prostopadle do powierzchni belki Belka naciska lewym końcem prostopadle do powierzchni poziomej Schematy statyczne podukładów i schematy obliczeniowe są zatem następu jące:

78

Statyku. 1.2.2 Wy/niic/onic reakcji * uMudutli płask ul'

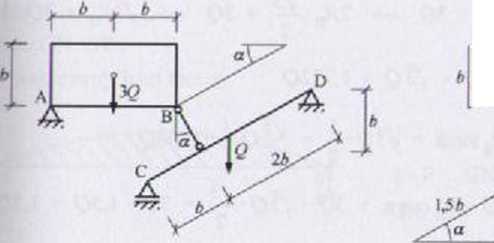
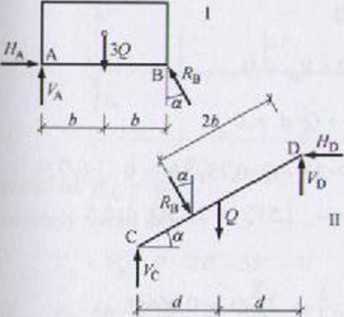
Bp/nofci geometryczne:

^ * \ -* O = 30°, coso = &

	—• c = 26 cos a = 26 - = fób
.i	=* d = 1,56 cos a - 1,56 *3L? = 2
Hy#tiłk'*enie reakcji: 1: 3RRS
V* o:	//A - Rh sin a =0
	Ka + Rbcosa - 3Q - 0
t «A • «>^	Rb cos a • 26 3Q • 6 ■ 0 |: 6

0,75v/3i

I 2.2. Wyznaczanie reakcji w układach phukich