Nowy 4 2

■208 4. Elektromagnetyzm

■208 4. Elektromagnetyzm

zatem

Powyższy wzór określa elementarną siłę dF działającą na element długości przewodnika dl. Całkowitą siłę działającą na przewodnik krzywoliniowy otrzymamy całkując wzór (4.62).

Działanie pola magnetycznego na obwód z prądem. Moment magnetyczny obwodu. Rozważymy obecnie działanie pola magnetycznego na zamknięty obwód elektryczny. Dla uproszczenia załóżmy, że obwód ma postać ramki ABCD o bokach a i b, ustawionej tak, że normalna do płaszczyzny obwodu tworzy kąt 0 z kierunkiem indukcji B (rys. 4.14). Siła wypadkowa działająca na

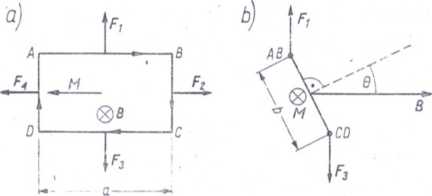
Rys. 4.14. Działanie pola magnetycznego na ramkę z prądem: a) ramka nie leży w płaszczyźnie rysunku, wektor indukcji B jest prostopadły do płaszczyzny rysunku, a wektor momentu skręcającego M leży w płaszczyźnie ramki, b) ten sam układ widziany z boku

obwód jest sumą sił działających na jego cztery boki. Stosując regułę śruby pra-woskrętnej przekonujemy się bez trudu, że siły F_l9 Fo, F₃ i F₄ są skierowane na zewnątrz ramki, jak pokazano na rys. 4.14. Siły F₂ i F₄ wzajemnie się znoszą. Wypadkowa sił F₁ i F₃ także jest równa zeru, ale tworzą one parę sił o momencie

M = F₁-^-sin6-\-F₃~sin 0

korzystając z wzoru (4.61) obliczmy wartość siły F_x (równą wartości F₃). Mamy

Fi = IaB

M = F_x b sin 6 = IaBb sin 0

Oznaczając przez 5 powierzchnię ramki (S = ab) możemy otrzymany wzór za-

pisać w postaci
	M = ISB sin 0	(4.63)
lub wektorowo	M = I (S-xB)	(4.64)

gdzie S oznacza zorientowany wektor powierzchni, tzn. wektor prostopadły do płaszczyzny obwodu o wartości równej polu powierzchni tego obwodu. Zwrot

\

wektora 5 zależy od kierunku prądu w obwodzie i jest określony według reguły śruby prawoskrętnej: jeżeli obracamy śrubę zgodnie z kierunkiem prądu, to jej nich wskaże zwrot wektora S.

Wzór (4.64) określa kierunek i zwrot wektora momentu siły M. W przypadku przedstawionym na rys. 4.14 wektor ten jest skierowany równolegle do boków AB i CD ramki. Pole magnetyczne działa zatem na zamknięty obwód z prądem momentem skręcającym. Ze wzoru (4.63) widać, że wartość tego momentu jest równa zeru, gdy 0 = 0, tzn. gdy ramka jest ustawiona prostopadle do wektora indukcji B. Położenie równowagi ramki występuje, gdy S II B.

Wyrażenie

H = IS    .    (4.65)

nazywamy dipolowym magnetycznym momentem obwodu albo w skrócie: momentem magnetycznym obwodu. Można tu powołać się na analogię z dipolem elektrycznym (patrz p. 4.1), który w polu elektrycznym ulega momentowi skręcającemu. Obwód z prądem można więc traktować jako dipol magnetyczny.

Korzystając z pojęcia momentu magnetycznego, wzór na moment siły możemy zapisać w postaci

M = pxB    (4.66)

Wzór ten jest słuszny dla obwodów dowolnego kształtu, a także dla innych typów dipoli magnetycznych, np. magnesów trwałych.

■* Z siłami działającymi na dipol związany jest pewien rodzaj energii potencjalnej, tzw. energia magnetyczna dipola. Można wykazać, że energia ta wyraża się wzorem

E_p = —flB    '    (4.67)

Pole magnetyczne przewodnika z prądem. Przemkalność magnetyczna. Jakościowy obraz pola magnetycznego uzyskujemy rysując tzw. linie wektora indukcji magnetycznej, zwane też liniami pola magnetycznego. Są to linie, do których w każdym punkcie styczny jest wektor B. Doświadczalnie linie te można wyznaczyć przy użyciu małych igiełek magnetycznych (dipoli magnetycznych), które, jak wiemy ustawiają się zgodnie z kierunkiem B. Umieszczając dużą liczbę takich igiełek w różnych punktach pola otrzymamy przybliżony obraz linii pola magnetycznego. Podobny rezultat uzyskamy stosując opiłki żelazne, które stają się dipolami w polu magnetycznym. Przy rysowaniu linii pola stosuje się umowę, że gęstość linii jest proporcjonalna do \B\.

Na rysunku 4.15 pokazano przebieg linii pola magnetycznego w otoczeniu prostoliniowego przewodnika ż prądem. Z rysunku widać, że w pobliżu przewodnika indukcja magnetyczna jest największa i maleje w miarę wzrostu odległości. Zwróćmy uwagę, że linie pola magnetycznego, wytwarzanego przez przewodnik z prądem są okręgami. Fakt, że linie pola magnetycznego są zamknięte, stanowi fundamentalną różnicę między polem magnetycznym a elektrycznym; przypominamy, że linie pola elektrycznego zaczynają i kończą się na ładunkach.

14 Fizyka