Photo013(1)

Funkcje Tornąuista I, II i III rodzaju. Funkcje T6mquista I, II i III ro<

przykładem funkcji hipcrbolicznych. Modele tego typu wykorzystywane w badaniach popytu konsumpcyjnego na trzy kategorie dóbr.

Funkcja TSrnąuista I rodzaju opisuje popyt na dobra konsumpcyjne ni: rzędu i dana jest wzorem: _ , ,

(2.

Y= ^a°^X +s, X + a,

przy założeniu: a₀ > 0, gdzie:

Y - zmienna objaśniana, wielkość popytu na badane dobro niższego rzędi X - zmienna objaśniająca, wielkość dochodu w badanym gosj domowym,

a₀ - stała (wyraz wolny), poziom nasycenia zmiennej objaśnianej Y, a, - parametr strukturalny,

€ - składnik losowy.

Wykres 2.5. Postać funkcji Tornąuista I rodzaju dla parametru q>0

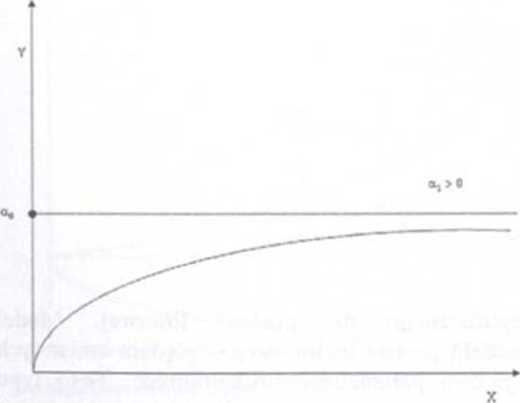
Żródto: Opracowanie własne.

Sprowadzenie modelu Tornąuista I rodzaju do postaci liniowej.

transformacji modeli Tornąuista dla ułatwienia przekształceń pomija się składnik | losowy (£).

Odwraca się obie strony równania:

1 _ 1 X + a_]

Y a_n X '

-U-fi+cj r ^a°\    .

podstawiając odpo

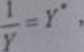
otrzymuje się

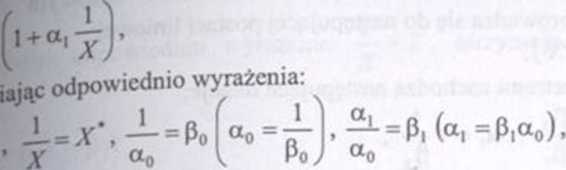
się postać liniową modelu:

(2.13)

modelu ekonomeirynntja

Y* =Po ⁺ P«^ •

Funkcja Tornąuista II rodzaju opisuje popyt na dobra konsumpcyjne wyższego rzędu i dana jest wzorem:

+    (2.15)

jr + a,

przy założeniu: ct₀,a₂ > 0, gdzie:

Y- zmienna objaśniana, wielkość popytu na badane dobro wyższego rzędu,

X - zmienna objaśniająca, wielkość dochodu w badanym gospodarstwie domowym,

a₀ - stała (wyraz wolny), poziom nasycenia zmiennej objaśnianej Y,

Oj.Oj - parametry strukturalne,

a_: - wartość przesunięcia wykresu funkcji na osi odciętych X, poziom zmiennej X przy którym pojawia się objaśniane zjawisko Y, t - składnik losowy.

Wykres 2.6. Postać funkcji Tómąuista II rodzaju

t

^ Oprać,

wanie własne.

x