Photo014(1)

Sprowadzenie modelu Tornąuista II rodzaju do postaci liniowej. M

Tómąuista II rodzaju z pominiętym składnikiem losowym (e) przekształceniach sprowadza się do następującej postaci liniowej:

J' = P₀+P,X₊P₂(KX),    ₍₂

gdzie między parametrami zachodzą następujące relacje:

Funkcja Tómąuista III rodzaju opisuje popyt na luksusowe dobra konsumpc i dana jest wzorem:

„ a_QX(X-a.₁)

Y = —2—^-— + 8,    (2

X+a,    ^v

przy założeniu: ot₀.a,,a₂ >0,

gdzie:

(oznaczenia jak we wzorze (2.15))

Y - zmienna objaśniana, wielkość popytu na badane dobro luksusowe.

X - zmienna objaśniająca, wielkość dochodu w badanym gospodarst domowym.

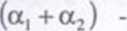
modelu.

wartość przecięcia osi odciętych przez asymptotę sk

✓

Y

/

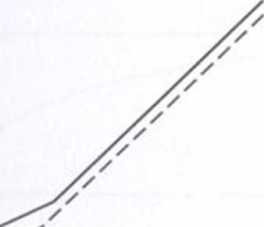
Wykres 2.7. Postać funkcji Tómąuista III rodzaju

—^-

O, / O,, a,

/

/

/

Źródło: Opracowanie własne.

Sprowadzenie modelu Tornąuista III rodzaju do postaci liniowej

Model Tómąuista III rodzaju z pominiętym składnikiem losowym (£) P°

przekształceniach sprowadza się do następującej postaci:

(2.18)

modelu:

Z*Po+Pi^ ⁺ P^2> ’

między param

P.

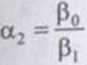
podstawiając odpowiednio

wyrażenie

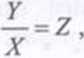
otrzymuje się postać liniową

ctrami zachodzą następujące relacje:

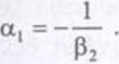
W przypadku, gdy nie jest znana postać analityczna funkcji badanego procesu, najczęściej stosowaną postacią wyjściową funkcji jest postać liniowa.

Jeżeli istnieje podejrzenie o nieprawidłowym doborze postaci analitycznej modelu

należy:    .......    ...    .

posłużyć się oceną wzrokową wykresu obserwacji i dobrać odpowiednią postać

analityczną, lub

- obliczyć współczynnik dobroci dopasowania oszacowanej funkcji do wartości obserwowanych, tzw. współczynnik determinacji R^: (współczynnik ten został omówiony w rozdziale 4.2, wzór (4.8)).

Współczynnik determinacji R^: przyjmuje wartości z przedziału (0;l). Pożądane są

wartości współczynnika R^: bliskie 1, świadczące o wysokim dopasowaniu oszacowanej funkcji do wartości rzeczywistych.

Przykład 2.2

Rozpatrzony został przebieg wartości zmiennej Y w czasie t = 1,2,...,12 (załącznik, tablica 2.2). Odpowiednią postać funkcji do modelu można dobrać posługując się oceną wzrokową wykresu zaobserwowanych wartości. Przebieg wartości zmiennej \ " jednostkach czasu t przedstawiono na wykresie 2.9.

podstawie wzrokowej oceny wykresu można stwierdzić, że kształt krzywej zbliżony jest do funkcji liniowej (wykres 2.1) lub do funkcji potęgowej (wykres 2.2).

39