pict0068b

Algebra z teorią liczb Informatyka I rok

21 Ki

20II r-

Kolokwium 2

[Aj

1. (5 pkł) Rozwiązać równanie macierzowe

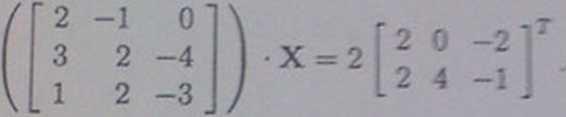
2.    (5 pkt) Rozwiązać układ rów nart stosując metodę Gaussa

2x    -    3y    -    3z    4-    t    -    2

—3x    4-    4 y    4-    z    4*    4f    =    0    .

x    -    y    4-    2z    -    5f    =    -2

3.    p£^ Obliczyć wyznacznik

2    3 3 3

3    2 3 3

3 3 2 3 *

3 3 3 2

<1. Niech przekształcenie liniowe T: R³ -» R^:i będzK dane nDCttr.

T (x, y_? z) = (x 4- y - 2z, -z - y 4- z, x - y).

(a)    pfc/j Znaleźć bazę jądra przekształcenia 7

(b)    fi pkt) Podać wymiar obrazu przekształcenia T

(c)    (2 pkt) Podać macierz przekształcenia 27 o 7 w "oazacń sanonicznych.

5. f<5 pkt) Określić w zależności od parametru p € R liczbę ror^ązań układu równań

px    4-    p*y    4-    z    =    -p

x    4-    y    -    pz    -    p² .

y    4-    z    =    1