Rotation of�

182

jest w tym przypadku tablicą implicentów. Rozwiązywanie tablicy Quine‘a odbywa się według algorytmu z rys. 3.21, przy czym określenia: i mp likant oraz jedynka funkcji, należy w nim zastąpić słowami, odpowiednio, implicent oraz zero funkcji.

Poszukiwanie minimalnej NPI funkcji zilustrujemy na przykładzie f unkcj i (3.62).

Przykład 3.16 (cd(l) Przykładu 3.15)

Funkcja (3.62), może być reprezentowana w sposób równoważny przez jej zera i “kreski":

y = f (x. ,x~,x.

_rx₂,x₃,x₄

) = 77 ^0,3,4,9.10.11.12 (5.8.13)J (3.63)

Jako rezultat Etapu I metody (rys. 3.24a) uzyskuje się następujące proste implicenty funkcji:

3,11(8);    0,4,8,12(4,8);

8,9,10,11(1,2)

4,5,12.13(1,8);    8,9,12,13(1,4);

(3.64)

W wyniku Etapu II (rys. 3.24b) generowany jest minimalny zestaw prostych implicentów funkcji nakrywających wszystkie jej zera. Są to implicenty (sposób określenia odpowiadających im elementarnych sum jest podobny do (3.54)):

3,11(8)

0,4,8,12(4.8)

8.9,10.11(1,2)

0011

0000

(x_+x_+x_/,)

'2 3    4

1000    (3.65)

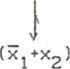
Minimalna NPI funkcji (3.63) jest następująca

y = f (Xj,x₂, ^x3>x₄

^x2’^x3’^x4^ ⁼ ^^x2 ^{+ x}3 ^{+ x}4^ (^y3 ⁺ ><4) (Xj * *₂)

(3.66)

a) Etap I (rozpatrywany jest zbiór u F )

Indeks	Kolumna 1	Kolumna 2	Kolumna 3
0	0 V	0,4(4) V 0,8(8) V	0,4, 8,12(4,8)
1	4 V 8 V		4,5,12,13(1,8) 8,9,12.13(1,4) 8,9,10,11(1,2)
		4, 5(1) V 4,12(8) V 8, 9(1) V 8,10(2) V 8,12(4) V
2	3 V 5 V 9 V 10 V 12 V
		3,11(8) * 5,13(8) V 9,11(2) V 9,13(4) V 10.11(1) V 12, 13( 1‘) V
3	11 V 13 V

b) Etap II (rozpatrywany jest wyłącznie zbiór F°)

Proste ^N\F^<"* implicenty	0	3	4	9	10	11	12
3,11(8)		V				V		*
0,4,8,12(4,8)	V		V				V	•
4,5,12.13(1,8)			V				V
8,9,12,13(1,4)				V			V
8.9,10,11(1,2)				V	V	V		•
	»	•	•	•	•	•	*

Rys.' 3.24. Minimalizacja NPI funkcji (3.63)