skanowanie0091 2

188 Optyka

3.    Nastawić lunetkę na ostrość widzenia linii rozgraniczającej pola oraz lupę.; odczytową na ostrość widzenia skali.

4.    Wstawić rurkę z czystą wodą do polarymetru.

5.    Obracając analizator, doprowadzić do równego (ciemnego) pola widzenia i: odczytać wskazanie kątomierza. W razie potrzeby powtarzać pomiar, każdora-J zowo obracając analizator o przypadkowy kąt i na nowo ustalając właściwe położenie.

6.    Umieszczać w polarymetrze kolejno rurki z roztworami o różnych stężeniach i odczytywać kąty podobnie jak w punkcie 5.

7.    Na papierze milimetrowym wykreślić zależność a=j[c).

8.    Obliczyć współczynnik nachylenia oraz jego błąd metodą regresji liniowej.

9.    Obliczyć właściwą zdolność skręcającą dla badanej cieczy, wykorzystując równanie (45.3).

10.Obliczyć błąd [a\ metodą różniczki zupełnej lub logarytmicznej.

11.Zaokrąglić wyniki obliczeń i przedstawić wynik w postaci ostatecznej.

Zestaw ćwiczeniowy

Polarymetr, lampa, rurki z wodą i roztworami

Pojęcia kluczowe

Polaryzacja liniowa, polaryzacja przez odbicie i załamanie, podwójne załamanie

Kryształy anizotropowe i izotropowe, oś optyczna

Pryzmat Nicola, dichroizm

Polaryzator i analizator, prawo Malusa

Polaryzacja kołowa i eliptyczna

Skręcenie płaszczyzny polaryzacji, węgiel asymetryczny

Polarymetr, przyrząd półcieniowy

Wzór Biota

Pomiary do wykonania, obliczenie właściwej zdolności skręcającej Noniusz (rozdz. 5)

46. Wyznaczanie stałej Stefana-Boltzmanna za pomocą pirometru

Wprowadzenie

Promieniowanie termiczne dowolnego ciała charakteryzuje się za pomocą tzw. zdolności emisyjnej r* Wielkość ta jest zdefiniowana w ten sposób, że ridX jest energią promienistą emitowaną w jednostce czasu przez jednostkową po-

46. Wyznaczanie stałej Stefana-Boltzmanna za pomocą pirometru

189

wierzch nię w wąskim przedziale długości fal (Z, Z + d)l). Zdolność emisyjna zależy od rodzaju ciała i jest funkcją temperatury oraz długości fali. Zależność zdolności emisyjnej od długości fali nazywa się również widmem promieniowania i jest opisanaprmwem Plancka:

(46.1)

r -^C|    1

* Z⁵ e^C2'^iT -1 ’

w którym Ci, C2 są pewnymi stałymi, k - stałą Boltzmanna.

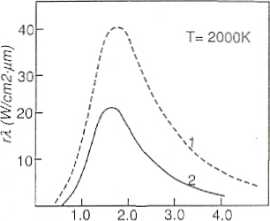
Rys. 46.1. Widmo promieniowania ciała doskonale czarnego (I) i ciała szarego (2)

Zdolność emisyjna dla wybranej temperatury i długości fali ma różne wartości dla różnych ciał, a wartość maksymalną osiąga w wyidealizowanym przypadku ciała doskonale czarnego. Wszystkie ciała rzeczywiste nazywamy szarymi. Widma promieniowania ciała doskonale czarnego i szarego w określonej temperaturze przedstawiono na rys. 46.1. Widzimy, że ciało szare charakteryzuje się kształtem widma identycznym z kształtem widma ciała czarnego, lecz mniejszą wartością r* dla każdej długości fali.

Dluaość fali (lim)

Na podstawie rys. 46.1 możemy stwierdzić, że ciało szare promieniuje tak samo jak ciało czarne o odpowiednio niższej temperaturze. Można mu przypisać właściwości ciała czarnego, jeżeli temperaturę rzeczywistą T_n zastąpić tzw. temperaturą czarną T_e.

Całkowita emisja energetyczna Re jest energią wypromieniowaną w jednostce czasu przez jednostkową powierzchnię w postaci fal o wszystkich możliwych długościach. Jej wartość

otrzymamy, całkując zdolność emisyjną rx względem wszystkich długości fal, od zera do nieskończoności:

R_c = i[r_AdZ.    (46.2)

0

Według prawa Stefana całkowita emisja energetyczna jest proporcjonalna do czwartej potęgi temperatury bezwzględnej.

R_c = oT⁴.    (46.3)

Współczynnik (7 nosi nazwę stałej Stefana-Boltzmanna.