skanuj0046 3

W_M Ac, a_b, aj = - - (l-p){ (^H)'^{-1 sin a}. “ ⁸/^sin aj ^Z Yc    , = 1

+ [8j (1+ — Ej) ⁺ 0,5 As (2 + Ej + + 0,5 Ae)] (^T(-l)^{1 1} sin a, - 5, sin a_b) +

i+i

1    ^m

+ - pAs (2 + Ej + As)[0,5 (^(-1)^,_1 a, - 8,a_b) +

^    u\

m

+ 0,25 (^(-l)'"¹ sin 2a,-8,sin 2aJ] +

/+i

1    ^m

+ — p² (Ae)² [^(-ir¹ sin a, - 5, sin a_b +

^    /+i i ^m

-- (S^¹)^1-' ^{sin3 a}i “ S/ sin³ aj]} +

^ó (+i

f    , fci

+ 0,5p-^ —{--(y(-l)^,_1sina + 8_fclsina_al) +

fck P Ys tt

1 ™

+- [(^Ei +Ae) ( V (-1)'*¹ sina, -8_fclsina_al) +

^ess    fcl + l

+ p_s Ae [0,5( £(-l)"' a, -8_fcla_al) +

fcl+1

+ 0,25( £(-l)^{M sin} 2a,.-8_fclsin 2a_al)]]}.    (7.34)

fci+i

7.4. Uwzględnienie uogólnionego prawa fizycznego betonu

i stali

W rozważaniach przedstawionych w tym rozdziale przyjęto bardziej ogólną postać związku fizycznego, uwzględniającego efekt osłabienia betonu. Zależność tę zinterpretowano graficznie na rysunkach 7.4 i 7.5, na których krzywą opadającą, opisującą zachowanie betonu w zakresie pla-•.tycznym, yprokNymowuno pioslą. Analityczny poslm ty li ule. nom i określają wzory

C

C,dzie:

7o e₀ ^2eo

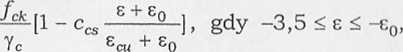
e₀ - parametr liczbowy,

f - f

c_cs -^Jcd_ ^Jcu - umowny współczynnik osłabienia betonu (ang. sof ^cd tening),

fcu - wartość funkcji opisanej wzorem (7.35)₂ dla e = E_m.

Rozważany zakres osłabienia betonu ściskanego (do 3,5%o) nie wy maga badania odciążenia uplastycznionej stali rozciąganej. W odniesie niu do stali zakładamy model sprężysto-plastyczny z uwzględnieniem wzmocnienia

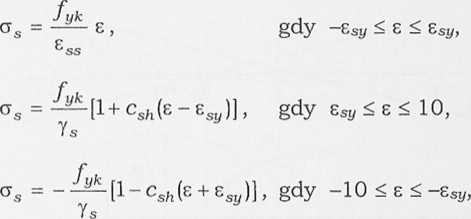
(7.36)

gdzie:

c_sh - umowny współczynnik wzmocnienia stali (ang. strain harde-ning) wyrażony wzorem:

ftd ~ fyd ®ud ~ ^esj/

(7.37)

f_d - obliczeniowa wytrzymałość stali zbrojeniowej na rozciąganie, e_ud - obliczeniowe odkształcenie stali równe 0,9 s_uk,

e_uk - charakterystyczne odkształcenie stali odpowiadające maksymalnej sile rozciągającej.