skan spr z TSiP

SPRAWDZIAN z ćwiczeń NR 1 - TSiP - 29.03.2012 - GRUPA B

Zadanie 1: Dla zagadnienia klina tarczowego, jak na rysunku,

podano funkcję naprężeń Airy’ego, w postaci: F{r,(p) = r-cp-cosę

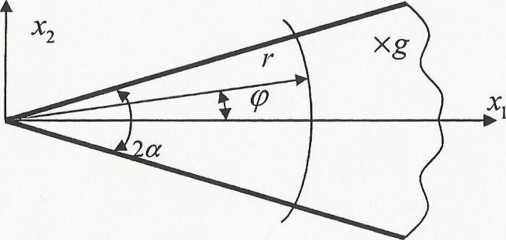
r,cp - współrzędne biegunowe

2 a - kąt wierzchołkowy

1)    Udowodnić, że podana powyżej funkcja naprężeń F(r,cp) spełnia równania nierozdzielności odkształceń zagadnienia 2-wymiarowego.

2)    Dane jest równanie biharmoniczne w układzie biegunowym: VlF(r,q>) = F(r,q>)„ + (r'¹)• F(r,ę)_r Ą^)-F{r,ę) _w.

Na jego podstawie obliczyć składową stanu naprężeń

(7

(pr

3) Udowodnić, że składowa stanu naprężenia a_rr dla zagadnienia zapisanego powyżej jest składową tensora naprężeń głównych.

4) Zakładając, że 2or = 180° oraz że P_A\\ do osi symetrii naszkicować wykres naprężeń (J_rr i podać jego ekstremalne wartości.

Zadanie 2: Dla zagadnienia elementu tarczowego (PSN) w układzie ortokartezjańskim odnaleźć stałe funkcji naprężeń Airy’ego (A,B,C) dla poniższego oddziaływania:

równomierne ścinanie w płaszcz. OxiX₂, o wartości 15MPa

Dane:

Funkcja naprężeń Airy’ego: F (jc, ,x₂) = A ■ xf + B • x^₂ + C • x\ .

_C1 . , _f    .    .    d²F    d²F    d²F

Składowe stanu naprężenia: <7_U =—— , <J₂₂ =—— oraz <J₁₂ =--

dx₂    dxf    dx_}dx₂

Zadanie 1: Dla zagadnienia klina tarczowego, jak na rysunku,

podano funkcję naprężeń Airy’ego, w postaci: F(r,<p) = r-cp-sincp

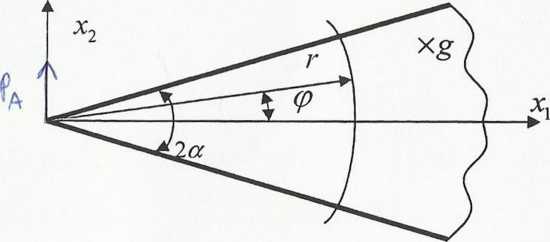
r,(p - współrzędne biegunowe

2 a - kąt wierzchołkowy

1)    Udowodnić, że podana powyżej funkcja naprężeń F(r,(p) spełnia równania konstytutywne zaproponowane przez Hooke’a.

2)    Dane jest równanie biharmoniczne w układzie biegunowym:

<P<P

V²F{r, ę) = F (r,<p)_j r+(r^_l )-F(r,ę)_r+{r~²)-F{r,ę)

rep

Na jego podstawie obliczyć składową stanu naprężeń

3) Udowodnić, że składowa stanu naprężenia dla zagadnienia zapisanego powyżej jest składową tensora naprężeń głównych.

4) Zakładając, że 2ćz = 180° oraz że P_A _L do osi symetrii naszkicować wykres naprężeń <T_n. i podać jego ekstremalne wartości.

Zadanie 2: Dla zagadnienia elementu tarczowego (PSN) w układzie ortokartezjańskim odnaleźć stałe funkcji naprężeń Airy’ego (A,B,C) dla poniższego oddziaływania:

rozciąganie osiowe wzdłuż osi x_l9 o wartości 30MPa

Dane:

Funkcja naprężeń Airy’ego: F(x,,x₂) = A-xj² +B-x_]x₂ +C-x₂ .

_Q1 . ,    ,    .    .    d²F    d²F    d²F

Składowe stanu naprężenia: a_u =—— , <j₂₂ =—— oraz cr₁₂ =--

dx₂    3x,    dx,dx₂