Snap11

Pogranicze i\-cia

przybiera albo wartość liczb całkowitych, albo połówkowych Cząstki o spinie zarówno całkowitym, bozony, jak i o spinie połówkowym, fermiony, dzielą się na te, które mogą brać udział w silnych oddziaływaniach, i te, które tej cechy nie posiadają. W silnych oddziaływaniach uczestniczą tylko mezony n i K oraz banony, nie uczestniczą zaś cząstki lekkie jak elektrony, fotony itp. Oddziaływanie cząstek na siebie i na inne cząstki, dokonujące się za pośrednictwem wytworzonego przez siebie pola (elektromagnetycznego, nuklconowego, mezonowego), wiąże się z pewną energią zgodnie ze wzorem Einsteina E - mc\ a więc i z pewną masą. Ze wzoru widać, że tak energia, jak i masa cząstek w ruchu będzie odpowiednio większa od masy cząstek nie działających (masa spoczynkowa). Zgodnie ze w-zorem Lorenza

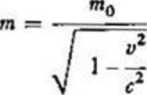
masa relatywistyczna m jest zawsze większa od masy spoczynkowej danej cząstki Zostało to stwierdzone w doświadczeniach z szybkimi cząstkami /?, cząstkami z substancji radioaktywnych i innymi cząstkami przyspieszonymi do wielkich prędkości w akceleratorach atomowych⁷⁶.

Rówmważność masy i energii jest powszechna i wskazuje na to, źc cząstka promieniująca energię traci równocześnie wskutek tego masę. Ta niewielka strata masy (1 g masy = 9 10*'^c erg) wyzwala ogromne ilości energii. Stwierdzenie równoważności masy i energii stało się istotnym krokiem w kierunku zrozumienia materialnej istoty promieniowania. Jeszcze przed powstaniem teorii względności stwierdzono pewną bezwładność energii elektromagnetycznej, a w mechanice kwantowej wzór E = nur uogólniono na wszystkie rodzaje energii.

Zgodnie z teorią kwantów promieniowanie posiada strukturę cząsteczkową, rozchodzi się w przestrzeni w postaci fotonów o energii hv (w równaniu fotoelcktrycznym Einsteina hv - Ej + \ 12 mir). Rzeczą doniosłej wagi było zastosowanie przez L. de Broglie*a teorii ruchu falowego do mechaniki kwantowej, co dało podstawy współczesnej mechanice falowej. W mechanice kwantowej każdej cząstce można przyporządkować określone zjaw-isko falowe, tak jak w przypadku światła*’⁷, które mając charakter falowy wykazuje zarazem cechy korpuskulame. Tak np. wiązka elektronów' może wykazywać zjawiska interferencji. E. Schródingcr wykorzystał te przejawy' kwantowo-falowe do określenia stanu kwantowego elektronów w atomie w równaniu, które opisuje rozchodzenie się fali towarzyszącej poruszającemu się np. elektronowi Stąd można obliczyć wartość ruchu elektronu w dowolnym miejscu pola.

Rozróżnienie między cząstką i falą istnieje raczej w sposobie obserwacji i opisu matematycznego niż w samej cząstce czy fali. Po prostu materia posiada sukcesywnie

’* Por. F. C. C h 3 m p i o n. H. Davy: Propen ies of mat ter, Londorv-Gl3sgow 1960. t ed.. 51; A. P. F r c n o h. Zasatły fizyki współczesne;, z ang ilum. A Wróblewski. Warszawa 1960, 166-168.

³’ Por. A. G. v a n Melscn: From atomos to atom. The history ofthe concept of atom. New York 1960, 174 n

Życie - ewotuga

własności tak korpuskulame. jak i falowe, i do tej pory to dualne ujęcie materii dobrze tłumaczy wiele faktów fizycznych, chociaż z drugiej strony kryje w sobie pewme trudności. Próba syntezy tego dualizmu w kierunku monistycznym, albo korpuskularnym, albo falowym, jest w fizyce współczesnej nadal sprawą otwartą.

Struktura cząsteczkowo-poiowa pozwala na dokładniejsze poznanie własności materii, jej indywidualności i różnorodności. Ze schematu widać, żc materia występuje

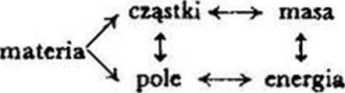
w postaci pola i wtedy jawi się jako energia. Masa i energia są ze sobą powiązane równaniem Einsteina; każda masa reprezentuje energię i vice versa. Podobnie oczywista korelacja istnieje między cząstką i polem, skoro według teorii polowcj każda cząstka jest właściwie skwantowanym polem. Cząstka oznacza więc maximum skupienia energii

w danym obszarze pola¹".

W porównaniu z klasyczną fizyką Newtona, która za podstawowe własności materii uważała masę (jako miarę bezwładności ciała), rozciągłość, nieprzenikliwość, przyspieszenie, siłę i wystarczała w zupełności do opisu makroświata, mechanika kwantowa, falowa i fizyka jądrowa wprowadziły istotne zmiany. W zakres pojęcia materii włączono 'także promieniowanie, światło, posiadające minimalną masę (a tym samym ważkość), korpuskuły uważane za cząstki materii teoria kwantowa mvaza za kwanty energii. Zmianie uległo również pojęcie rozciągłości i nieprzenikałności, zwłaszcza pod wpływem stwierdzenia faktu, że pola mogą się na siebie nakładać w tym samym obszarze przestrzeni. Teoria pola wyeliminowała pojęcie bezpośredniego oddziaływania na odległość.

2.2.2. Charakterystyka materii ożywionej

Już potoczna obserwacja pozwala na wyróżnienie wśród obiektów przyrody tych, które zaliczamy do świata istot żywych. Kiytcrium stanowią tu właściwości ustroju żywego, a więc odpowiedni kształt i wielkość, przyswajanie i wydalanie substancji pokarmowych (metabolizm), wzrost masy i objętości ciała, zdolność do rozmnażania się i przekazywania cech dziedzicznych potomstwu, stopniowy rozwój osobniczy, ruch,, pobudliwość, plastyczność przystosowawcza, zmienność i ewulucja czy wreszcie śmierć jako całkowity zanik czynności życiowych.

Jednak przy bliższej analizie powstaje pytanie, czy te cechy lub ich suma stanowią istotny i dostateczny wskaźnik do odróżnienia materii żywej od nieożywionej. Trudności te wzrastają, gdy mamy w pamięci to, co powiedziano o jednorodności elementów materialnych tych dwóch światów, oraz to, że wiele własności tych cech wyjaśniono już

³‘ D. B ł o c h i n c c w: Pwlslawy mechaniki kwantowej, tłum. r. roi.. Warszawa 1954.465-467.

303