skan0044

103

Mamy wlflC

M 1 4/*-i	[2 2
L(3^a + 4)^aJ "	[s^2 + 4 s^2 + 4j	1

l / Min 2{t - ■ t)hui 2rar

4 / [sin 2t sin 2r cos 2r — cos 24 sin² 2r]dr = — 2t cos 2t + sin 2t, Jo

2. St oh ująć transformatę Laplace’a do równania różniczkowego i korzystając w wzoru (2.12.1) i warunków początkowych, mamy

«^!,V(/<)-s^a2/(0)-sy^,(0)-/(0)-[s²F(s)-s2/(0)-3/^,(0)]-[sF(s)-2/(0)]+y(s) =

3- i

a stąd

F(s) =

(s-l)³(3 + l)'

Funkcję F rozłożymy na ułamki proste:

A B    CD

+ i-rrrr + |-iH +

(s^l)³(s + l) 3— 1    (s-1)²    (S-1)³    3 + 1

a stąd

6 = A(s- 1 )²(s + 1) + B(s² - 1) + C{s + 1) + D(s - l)³. Porównując współczynniki przy tych samych potęgach s, mamy

6=A-B+C-D 0 = A-2A + C + 3D 0 = -A + B — ZD 0 = A + D

a więc

§j C = 3, D = —f. Stąd i z własności

C[e^atf(t)] = F(s - a) przy F{s) = £[/(*)] otrzymujemy szukane rozwiązanie

*•[!+]

a.v

W,

3 1 43 + 1

Wyznaczyć rozwiązanie równania całkowego:

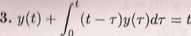
Niech f(t) — t. Wtedy powyższe równanie można zapisać w postaci y(t) + f*y = t

i stosując do niego przekszałcenie Laplace’a, otrzymamy

y(«) + WW = 4.

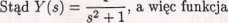
y (£) = sin t

jest szukanym rozwiązaniem.

Stosując przekszałcenie Laplace’a, wyznaczyć rozwiązania następujących problemów:

2. y' - 3y = e^2t, y(0) = 1 4. y' - 2y = 4, y(0) = 3 6. y' -ł- 4y = e^-4*, y(0) = 0

l-y^/-2/ = ¹> 3/(0)-°

3. y' + 2y = t, 2/(0) = -1 5. _y> _y = sint, 2/(0) — 0

7.    y" + 5y' + 4y = 0, y(0) = 0, y'(0) = 0

8.    y" - 6y' + 132/ = 0, 2/(0) = 0, y'(0) = -3

9.    _y» + 4/ + 4y = 0, 2/(0) = 0; 3/'(0) = 5

10.    y" + 62/' + 2521 = 0, y(0) = 2, y'(0) = 3

11.    y" - 62i + 92/ = *» 2/(0) = °» 2/'(0) = ¹

12.    y" + 22/' + V - ^{4 +} H ⁼ °»    ^{= 0}

13.    y" + y' = t³ + 2*. 2/(0) = 4, y'(0) = -2

14.2/" - 4y^# + 4y • t*. 2/(0) = 1.    = ⁰

15.y"-2l/'*M/-«^V» »(0) - 0. i/^#(0) - 0

10.    y" - 4y' 14y - tV, V<0) - 0, y'(0) - 0