str (

TRANSFORMACJE Transformacja położenia przez przeniesienie

Przeniesieniem poziomym figury nazywamy takie jej przejście do nowego położenia, w którym żaden jej punkt nie zmienia wysokości.

^ Przeniesieniem czołowym figury nazywamy takie jej przejście do nowego położenia, w którym żaden jej punkt nie zmienia głębokości.

Niech dane będą dwa różne punkty A i B dowolnie położone na figurze T. Przy przeniesieniu poziomym (czołowym) figury /"odległość punktów A i B nie ulega zmianie. Ponieważ nie zmieniają się także wysokości (głębokości) punktów A i B> zatem nie zmienia się długość rzutu poziomego (pionowego) odcinka AB. Wynika stąd natychmiast następujące twierdzenie:

Przy przeniesieniu poziomym (czołowyrń) figury nie ulega zmianie ani wielkość, ani kształt jej rzutu poziomego (pionowego).

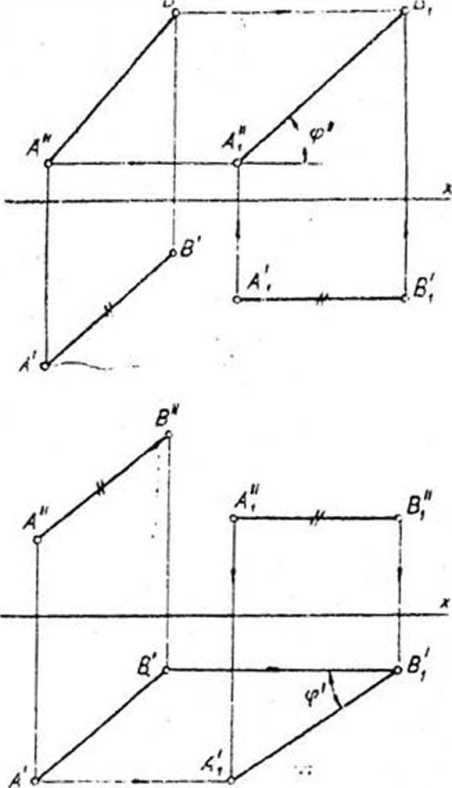
PRZYKŁAD 1. Dany odcinek ~AB    ustawić prostopadle do rzutni n_x.

Odcinek A~B sprowadzamy przez przeniesienie poziome najpierw do położenia rówr ległego do rzutni 7r₂, a następnie przez przeniesienie czołowe ustawiamy go prostopac do rzutni n_x.

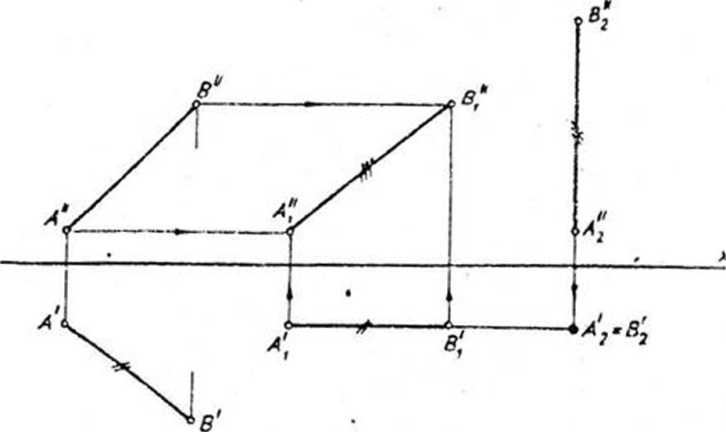
PRZYKŁAD 2. Wyznaczyć wielkość trójkąta ABC

Transformacja układu odniesienia

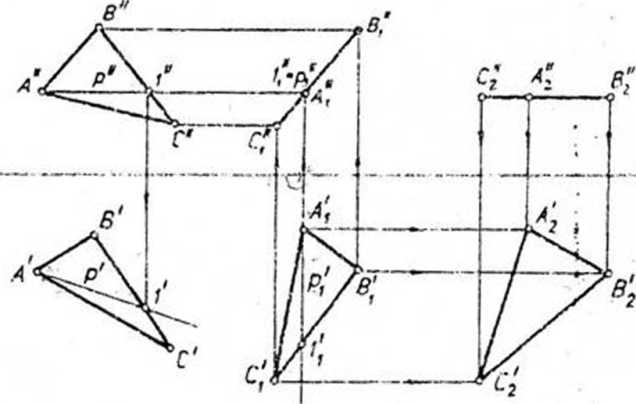
W prostokątnym układzie odniesienia x(n_x ,n₂) niech dana będzie płaszczyzna po-ziomo-rzutująca 7r₃, która przecina rzutnię n_x wzdłuż prostej x_x    Płaszczyznę

n2 nazywamy trzecią rzutnią, a prostą — osią rzutów nowego układu odniesienia x_x{n_x, 7r₃). Jeśli dla dowolnego punktu A wyznaczymy jego trzy rzuty prostokątne: pierwszy

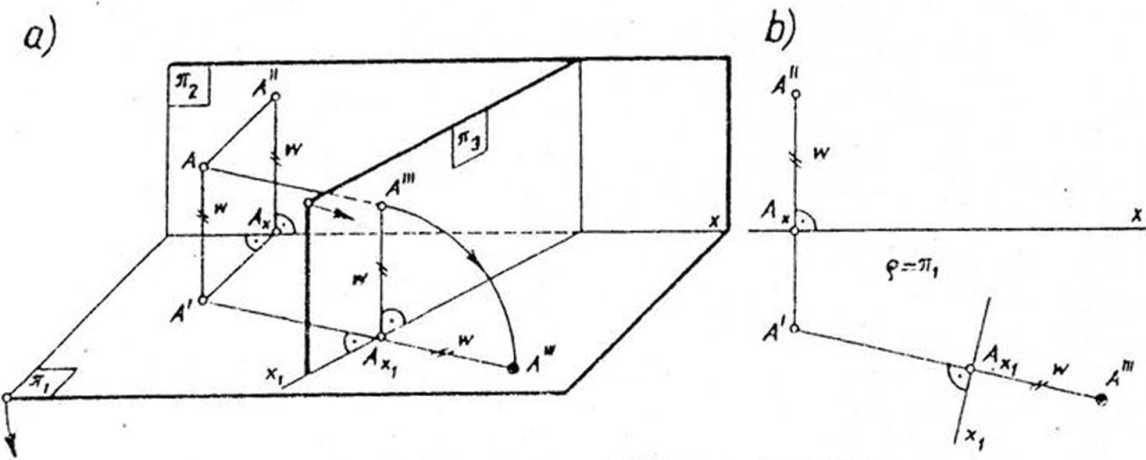
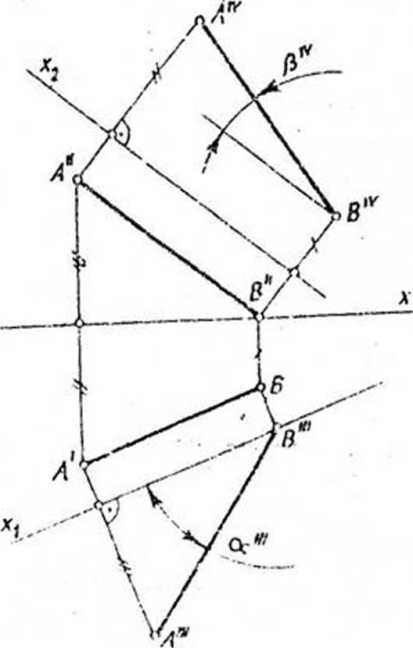
PRZYKŁAD Dany jest rzut poziomy i pionowy odcinka AB    . Wyznaczyć

kąty nachylenia odcinka AB do rzutni n₁ i n₂.

Wprowadząmy pomocniczą rzutnię n_z\_n_x i równoległą do odcinka.AB (x_x\\A'B). Wyznaczamy trzeci rzut odcinka AB.

Uzyskany kąt ct!"- £(.A'"B"\ x_x) równy jest szukanemu kątowi cc- £(AB, 7t_x)_f przy czym (AB)=(A"'B^f").