Untitled2 2

I

I

1111

2 analizy II - 19 06 04

1 Wyznaczyć całkę ogólną równania

</) y^,,-6.v^,*9>- - —    (//) yⁿ-2y‘+4y'-$y = 2e^iM

2. (1) Obliczyć masę bryły V - {(x,yx^: *y^: + r^: £ 2 a z £ _N/x-^:    }

jeśli gęstość masy fi(x, - 2r.

,0

' (U) Obliczyć objętość i pole powierzchni bryły ograniczonej powierzchniami —' z=9-)C-y^ł i z= 5

3    (1) Wykazać, ze całka J(y^: +r^: )Jx - 2y(x +c)dy +    + 2xryi:

r

nie za) czy oó drogi całowania oraz o*DUCzyć tę całkę, jcśYi K jest óowoinąkrzywą regularną o początku A(0,1,-I) i końcu B( 1,2,0).

(II) Sformułować twierdzenie o zamianie całki krzywoliniowej skierowanej na oznaczoną oraz obliczyć pracę siły F = Lv^:,l, :) wzdłuż drogi A' r(t) = [! + cos/. »n/. 2-cos/] od punktu A(2,0,l) do B(0,0,3).

4    (!) Sformułować twierdzenie o zamianie całki powierzchniowej zorientowanej na podwójną

oraz obliczyć całkę J j WńdS. jcsli W =\.r, -y, :]. natomiast S jest dolną stroną

s

powierzchni trójkąta o wierzchołkach A(ó.0,0), 13(0,2.0) i C(0,0.3)

(II) Sformułować twierdzenie Stokesa i stosując je obliczyć cyrkulację wektora W = [ ;\6x,y' ] wzdłuż krzywej K będącej brzegiem trójkąta o wierzchołkach A( 1,0,0). B(0,1.0) i C(0,0,1)

y (r-3)" “ (2/i >5)2-

5 (I) Wyznaczyć promień i przedział zbieżności szeregu

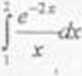
(II) Metodą rozwinięcia w szereg obliczy ć całkę

6 (I) funkcję /(;r) = e’^x przedstawić Z3 pomocą wzoru całkowego Fouriera

\

I 01) Funkcję f(x) - r(x x) rozwinąć w przedziale (O,*) w szereg Fouriera sinusów