WM009

Wielkość geometryczna J_y charakteryzuje opór, jaki belka stawia siłom odkształcającym w zależności od kształtu i wymiarów jej przekroju poprzecznego.

Wielkość fizyczna E charakteryzuje opór, jaki belka stawia siłom odkształcającym w zależności od własności fizycznych materiału, z którego jest ona wykonana.

Iloczyn EJ_y nazwano sztywnością belki na zginanie lub krócej sztywnością zginania.

Odkształcenie osi belki powoduje obroty poszczególnych jej przekrojów. Wykorzystując zależność [9-6] możemy wyznaczyć wzajemny kąt obrotu przekrojów 1-1 i 2-2 (rys. 9-5)

A zatem odkształcenia belki przy zginaniu są proporcjonalne do wartości momentu zginającego M_a i odwrotnie proporcjonalne do sztywności belki na zginanie. Zwróćmy uwagę, że gdyby nawet w rozpatrywanym przekroju belki istniała siła poprzeczna T_ay to wywołane tą siłą naprężenia styczne r_xz nie weszłyby do równań [9-3], [9-4] i [9-5], a więc równania te zachowałyby ważność w przypadku zginania z udziałem siły poprzecznej.

Podstawiając do wzoru [9-2] zależność [9-6] otrzymamy

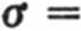
Ez M_az

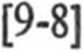
gdzie: M_a — moment zginający w rozpatrywanym przekroju, z — odległość od osi obojętnej y do punktu, w którym oblicza się naprężenie, J_y — moment bezwładności przekroju poprzecznego belki względem osi obojętnej.

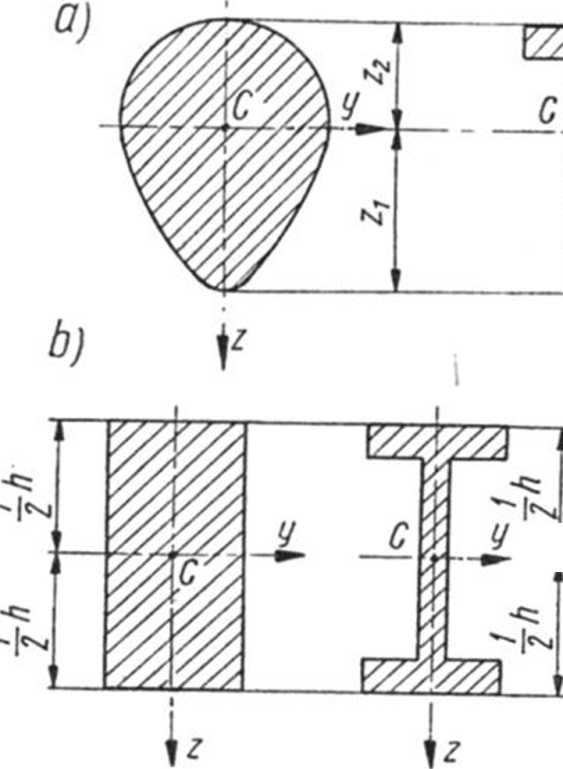
Ze wzoru tego wynika, że naprężenia normalne o zmieniają się liniowo na wysokości przekroju belki i ekstremalne ich wartości występują w skrajnych włóknach najbardziej odległych od osi obojętnej. Wykresy naprężeń o pokazano na rysunku 9-7.

m * y
N

x ^N Mc

— (5/7io x

(X

<5(f

—.    —C\—Z

ł

|«Xl

Rys. 9-7